Функциональное уравнение

[kp9r4d]

Найти все функции $f : \mathbb{R} \to \mathbb{R}$, такие, что $\forall x,y \in \mathbb{R} : f(x+y^2) = f(x) + f^2 (y)$
Довольно несложными рассуждениями, можно показать, что для любого $q \in \mathbb{Q}$ существуют лишь две функции:
$f_1(q) = q$
$f_2(q) = 0$

(Оффтоп)

Перепишем условия так $fx+yy = fx + fyfy$, при $x=0$ сделаем следствия:\\

$$f0 = f0 + f^2 0 \to f^2 0 = 0 \to f0 = 0$$

$$fxx =fxfx \to fx+yy = fx + fyy$$

$$f(x+z) = fx + fz, z \geqslant 0$$

$$0=f(-x+x)=f(-x) + f(x) \to -f(-x)=f(x)$$

Из последнего следствия видно, что $f$ однозначно определяется лишь положительной полуосью.

$$f1 = f^2 1 \to f1 = 0 \vee f1 = 1$$

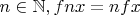
Очевидно также, что $n \in \mathbb{N}, fnx = nfx$ и в силу доказанной нечётности $fnx = nfx$ даже когда $n \in \mathbb{Z}$.\\
Докажем ещё, что $f(\frac{1}{n} x) = \frac{1}{n}f(x)$ когда $n \in \mathbb{Z}$, это следует из равенств

$$f(x) = f(\frac{n}{n}x) = nf(\frac{1}{n}x)$$

$$\frac{1}{n}f(x) = f(\frac{1}{n}x)$$

Из предыдущих двух утверждений, следует что $f(q) = qf(1)$ когда $q \in \mathbb{Q}$.

как обобщить результат на вещественные числа?

[ИСН]

По непрерывности. А если её нет, то увы.

[kp9r4d]

Понятно, спасибо.

[B@R5uk]

kp9r4d, что-то вы совсем замудрили. Тут вообще к целым обращаться не надо. Положите игрек нулю и посмотрите, чему равна функция в нуле. Потом положите икс нулю и найдите саму эту функцию (получатся уже найденные вами решения, только для любых действительных чисел).

[ИСН]

kp9r4d ровно, буквально, именно это и делает. Читайте букв.

[kp9r4d]

ИСН
Для читателей в будущем - таки не увы. Это отображение сохраняет квадрат и сложение, а значит монотонно, а значит решения-таки только два.