Возведение мощностей в степень

[Daft]

В книге Н.К. Верещагин, А.Шень "Начала теории множеств" (ftp://ftp.mccme.ru/users/shen/logic/sets/part1.pdf) на странице 37-38 говорится следующее:

Цитата:

Теперь определим возведение в степень. Для этого рассмотрим(для данных $A$ и $B$) множество всех функций вида $f:B\to A$ (напомним: это означает, что их область определения есть $B$, а область значений содержится в $A$). Это множество обозначается $A^B$, и его мощность и будет результатом операции возведения в степень. Если множества $A$ и $B$ конечны и содержат $a$ и $b$ элементов соответственно, то $A^B$ содержит как раз $a^b$ элементов. В самом деле, определяя функцию $f:B\to A$ , мы должны определить её значение на каждом из $b$ элементов. Это можно сделать $a$ способами, так что получаем всего $a^b$ вариантов.

.Объясните,пожалуйста,почему это верно. У меня не совпадает множество всех функций вида $f:B\to A$ с числом,которое получается при возведении в степень $A^B$ . Я не понимаю последнего предложения,ведь возведение числа в степень не имеет такого смысла,которой указывает автор.

[Xaositect]

Daft в сообщении #825247 писал(а):

.Объясните,пожалуйста,почему это верно. У меня не совпадает множество всех функций вида $f:B\to A$ с числом,которое получается при возведении в степень $A^B$ . Я не понимаю последнего предложения,ведь возведение числа в степень не имеет такого смысла,которой указывает автор.

А что получается у Вас?

Если у нас есть конечные множества $A$ и $B = \{p_1,\dots,p_b\}$, то любую функцию из $A^B$ можно задать таблицей ее значений:
\begin{tabular}{c|c} $p_1$ & $f(p_1)$ \\ $p_2$ & $f(p_2)$ \\ \dots & \dots\\ $p_b$ & $f(p_b)$ \end{tabular}
В правом столбце на каждое место можно поставить любой из $a$ элементов множества $A$, получается всего $a^b$ возможных таблиц.

[Daft]

Я что-то плохо понимаю,как вы объединили множество $A$ и $B$,возможно тут причина в том,что я не понимаю смысла выражения множество всех функций вида $f:B\to A$.Я задавал множество так(учитывая то,что перед этим была тема функции,где она определялась как упорядоченная пара $\langle b,a \rangle$),например: множество $A=\{1,2\}$ и $B=\{3,4\}$,тогда 1 множество это \{$\langle 1,3 \rangle,\langle 2,4 \rangle\} и второе множество \{$\langle 1,4 \rangle,\langle 2,3 \rangle\}. Получается 2 множества.Объясните пожалуйста мне,что я делаю не так и скажите я больной?

[ИСН]

Ездят на велосипеде. Попытка ездить на бутерброде обычно кончается неудачей: скорость маленькая, зад вымазан икрой.

-- менее минуты назад --

А, нет, я Вас не так понял. Почти всё правильно, но есть нюанс.

-- менее минуты назад --

А нюанс вот какой: кто сказал, что все значения функции должны быть разными?

[Daft]

Я не понял,вы говорите про инъективность?

[Xaositect]

Давайте разбираться с функциями. (То, что я пишу, немного отличается от Верещагина-Шеня, я определяю функции с областью определения $X$)

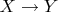
Неформально, функция $X\to Y$ - это правило, которое каждому элементу $x\in X$ мы ставим в соотвестствие ровно один элемент $y\in Y$. Для того, чтобы формализовать это определение в теории множеств, мы определяем функцию как множество пар: если функция $f$ сопоставляет элементу $x$ элемент $y$, то пара $\left<x, y\right>$ будет принадлежать нашей функции.

То есть: $f\colon X\to Y$ значит, что $f$ - это множество пар, то есть $f\subset X\times Y$, и для каждого элемента $x\in X$ в этом множестве есть единственная пара, связывающая его с каким-то $y\in Y$. Итак, по определению

$$f\colon X\to Y \stackrel{\mathrm{def}}{=} f\subset X\times Y \textrm{ и } \forall x\in X \exists! y\in Y \left<x, y\right> \in f.$$

$$y = f(x) \stackrel{\mathrm{def}}{=} \left<x, y\right> \in f.$$

Но это определение нужно нам только для формального обоснования, а интуитивно функция - это когда для каждого $x\in X$ есть ровно один "свой" $y\in Y$, который мы обозначаем $f(x)$. При этом ничего не сказано про то, что у разных иксов должны быть разные игреки. Также ничего не говорится про то, что игреки должны встречаться, это требуется только от иксов. То есть, например, $\{\left<0, 0\right>, \left<1, 0\right>\}$ - это корректная функция $\{0,1\}\to \{0,1\}$.

Соответственно, $A^B$ --- это множество всех функций $B\to A$, т.е. $\{f|f\colon B\to A\}$. Например,

$$\{0, 1\}^{\{2,3\}} = \{ {\color[rgb]{0.5,0,0}\{\left<2, 0\right>, \left<3, 0\right>\}}, {\color[rgb]{0,0.5,0}\{\left<2, 0\right>, \left<3, 1\right>\}}, {\color[rgb]{0,0,0.5}\{\left<2, 1\right>, \left<3, 0\right>\}}, {\color[rgb]{0,0.5,0.5}\{\left<2, 1\right>, \left<3, 1\right>\}}\}$$

Писать функции в виде множеств не очень удобно, поэтому обычно их задают другим способом. Я в предыдущем посте приводил табличное задание дискретной функции. В виде множества таблица \begin{tabular}{c|c}$p_1$ & $q_1$ \\ $p_2$ & $q_2$ \\ \dots & \dots\\$p_b$ & $q_b$\end{tabular} будет записана как $\{\left<p_1, q_1\right>, \left<p_2, q_2\right>, \dots, \left<p_b, q_b\right>\}$. Здесь $q_i = f(p_i)$ - это какие-то элементы, не обязательно различные.

[ИСН]

Daft в сообщении #825264 писал(а):

Я не понял,вы говорите про инъективность?

Можно сказать и так, да.

[Daft]

Я тоже так думал,но ведь $Y$ это множество значений,следовательно у каждого из элементов множества $Y$ должен быть свой прообраз?
Xaositect объясните мне пожалуйста,почему:

Цитата:

В правом столбце на каждое место можно поставить любой из $a$ элементов множества $A$, получается всего $a^b$ возможных таблиц.

Я не понимаю на каком основании это можно сделать?Объясните,пожалуйста, учитывая обозначения предыдущего поста.

[Xaositect]

Daft в сообщении #825271 писал(а):

Я тоже так думал,но ведь $Y$ это множество значений,следовательно у каждого из элементов множества $Y$ должен быть свой прообраз?

$Y$ - это не множество значений. $Y$ называется кодоменом.

У нас есть $b$ элементов множества $B$. Для первого элемента $b_1\in B$ есть $a$ вариантов выбора $f(b_1)$, для второго - тоже $a$ вариантов, и так далее. В итоге $a\cdot a\cdot \dots\cdot a = a^b$ вариантов.

[Daft]

Я понял про множество значений,просто в учебники говорилось,что при таком обозначении отображения множество $B$ это область определения,но когда говорилось про эту тему,то там было написано,что это обозначение,в данном случае,не имеет предыдущего смысла(А я пропустил это).

Цитата:

У нас есть $b$ элементов множества $B$. Для первого элемента $b_1\in B$ есть $a$ вариантов выбора $f(b_1)$, для второго - тоже $a$ вариантов, и так далее. В итоге $a\cdot a\cdot \dots\cdot a = a^b$ вариантов.

В учебнике написано тоже самое,но я не понимаю,разве это будет не сумма вариантов,а произведение?

[Xaositect]

Daft в сообщении #825275 писал(а):

Я понял про множество значений,просто в учебники говорилось,что при таком обозначении отображения множество $B$ это область определения,но когда говорилось про эту тему,то там было написано,что это обозначение,в данном случае,не имеет предыдущего смысла.

Там явно написано:

Daft в сообщении #825247 писал(а):

(напомним: это означает, что их область определения есть $B$, а область значений содержится в $A$)

Daft в сообщении #825275 писал(а):

В учебнике написано тоже самое,но я не понимаю,разве это будет не сумма вариантов,а произведение?

Да.

Например, если есть 10 вариантов выбрать первую букву, и десять вариантов выбрать вторую, то всего получится 100 двухбуквенных сочетаний.

[Daft]

Xaositect в сообщении #825276 писал(а):

Daft в сообщении #825275 писал(а):

Я понял про множество значений,просто в учебники говорилось,что при таком обозначении отображения множество $B$ это область определения,но когда говорилось про эту тему,то там было написано,что это обозначение,в данном случае,не имеет предыдущего смысла.

Там явно написано:

Daft в сообщении #825247 писал(а):

(напомним: это означает, что их область определения есть $B$, а область значений содержится в $A$)

Да,я просто слово содержится неправильно прочитал(задал тот смысл,какой сам захотел )
Спасибо большое,вы очень помогли мне.
Я действительно не задумывался над тем,что: если есть 10 вариантов выбрать первую букву, и десять вариантов выбрать вторую, то всего получится 100 двухбуквенных сочетаний . Очень мне стыдно,что я не знал этот факт и не задумывался над ним,хотя мне он кажется неочевидным.А вам? Столько проблем от моих глупых ошибок.Спасибо большое!

[Xaositect]

Daft в сообщении #825279 писал(а):

Очень мне стыдно,что я не знал этот факт и не задумывался над ним,хотя мне он кажется неочевидным.А вам?

Я слишком часто видел и использовал эту вещь, я уже не помню, казалась ли она мне когда-нибудь неочевидной. Можете представить прямоугольную таблицу типа такой, может, станет очевиднее:
\begin{tabular}{c|cccc} & A & B & C & D\\ \hline A & AA & AB & AC & AD\\ B & BA & BB & BC & BD\\ C & CA & CB & CC & CD\\ D & DA & DB & DC & DD \end{tabular}