Интеграл Даниеля

[djuuj]

В книге Шилов Г.Е., Гуревич Б.Л. - "Интеграл, мера и производная. Общая теория" - 1967 на с. 31 написано следующее, без доказательства:
Класс $L^+$ вместе с функциями $f$ и $g$ содержит $\min (f,g)$ и $\max (f,g)$.
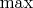
Для $\min (f,g)$ доказать легко, а вот для $\max$ я что-то не могу доказать.

Коротко о классе $L^+$. Пусть $H$ -- линейное пространство вещественнозначных функций $h\colon X\to \mathbb R$ такое, что $h\in H\Rightarrow |h|\in H$ (пространство элементарных функций), $I$ -- положительно определённый линейный непрерывный функционал на $H$ (интеграл от элементарных функций). Функция $f(x)$ (принимающая, возможно, и бесконечные значения) по определению принадлежит классу $L^+$, если существует такая последовательность функций $h_n(x)\in H$, что $h_n\nearrow f$, причём интегралы функций $h_n$ ограничены в совокупности: $Ih_n\le C$.

[djuuj]

Забыл сказать, функции $h\in H$ ограничены.

[Dan B-Yallay]

djuuj в сообщении #825132 писал(а):

Для $\min (f,g)$ доказать легко, а вот для $\max$ я что-то не могу доказать.

$\max (f, g)= -\min (-f,-g)$

[djuuj]

Dan B-Yallay в сообщении #825170 писал(а):

djuuj в сообщении #825132 писал(а):

Для $\min (f,g)$ доказать легко, а вот для $\max$ я что-то не могу доказать.

$\max (f, g)= -\min (-f,-g)$

$-f$ не обязательно входит в $L^+$, в книге это отмечено.
На всякий случай уточню, что $h_n\nearrow f$ означает $h_1\le h_2\le\ldots,\ h_n\to f$.

[Dan B-Yallay]

Интеграл Даниеля не изучал, поэтому знаю не больше вас. Давайте попытаемся решить вместе. Есть ли проблема в таком наивном подходе:

$$\begin{align}f,g \in L^+ \quad \Rightarrow \quad \exists h_n, k_n \in H: \ \ h_n \nearrow f,\ k_n \nearrow g \\ \forall h,k \in H: \ \ \min(h,k), \max(h,k) \in H \\ \varphi_n=\min(h_n, k_n) \nearrow \min(f,g) \ (??) \\ \psi_n=\max(h_n,k_n) \nearrow \max(f,g) \ (??) \end{align}$$

[djuuj]

Dan B-Yallay в сообщении #825396 писал(а):

Интеграл Даниеля не изучал, поэтому знаю не больше вас. Давайте попытаемся решить вместе. Есть ли проблема в таком наивном подходе:

$$\begin{align}f,g \in L^+ \quad \Rightarrow \quad \exists h_n, k_n \in H: \ \ h_n \nearrow f,\ k_n \nearrow g \\ \forall h,k \in H: \ \ \min(h,k), \max(h,k) \in H \\ \varphi_n=\min(h_n, k_n) \nearrow \min(f,g) \ (??) \\ \psi_n=\max(h_n,k_n) \nearrow \max(f,g) \ (??) \end{align}$$

Всё правильно, но в определении класса $L^+$ есть ещё такое условие:

djuuj в сообщении #825132 писал(а):

интегралы функций $h_n$ ограничены в совокупности: $Ih_n\le C$

Вот здесь то я и завис, как доказать ограниченность интегралов $I\max (h_n, k_n)$ вообще без понятия. Для $\min$ это следует из монотонности $I$ на $H$ и того, что $\min (h_n, k_n)\le h_n$.