на мой взгляд 1 и 2 задачи имеют вообще разные решения.
В чем состоит эксперимент первой задачи --- вы смотрите на прибор, определяя сколько блоков вышло из строя.
В первой пространство элементарных исходов содержит в себе следующие исходы:
все работает:
1 нет, 2,3 да;
2 нет, 1,3 да;
3 нет, 1,2 да;
1,2 нет, 3 да;
1,3 нет, 2 да;
..................
ничего не работает.
Число исходов конечно

. Вам нужно найти, что отказало два блока из трех --- это соответствует 3 элементаным исходам.
Вероятность их суммы равна сумме их вероятностей.
Т.к. выходы из строя каждого блока независимы, то нужно перемножить соответствующие вероятности. Для примера --- вероятность выхода из строя 1 и 2 блока

Полученные три числа нужно сложить.
Во 2 задаче уже известно, что два блока вышли из строя. Эта задача решается по формуле полной вероятности.
Событие А --- выход из строя 2 блоков из трех
Введем 3 гипотезы
Н1 --- вышли из строя 2,3 блоки.
Н2 --- вышли из строя 1,3 блоки.
Н3 --- вышли из строя 1,2 блоки.
Вероятность каждой гипотезы, а они равновозможны --- 1/3.
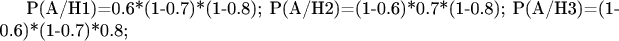
Они уже должны быть подсчитаны в решении первой задачи. Затем по формуле Байеса находите, что требовалось.