Вы меня расстраиваете...
как вообще может получится конечный предел , если t -> 0.
Представьте, что

, а

(ведь

при некоторых углах стремится к бесконечности, а

отклонение от одного из таких углов). Тогда

при любом ненулевом

, а предел константы ей же и равен.
Извините, но я не понимаю, как работать с t в данном случае и к чему в таком случае стремится
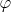
в

(при r)
На примере найденного угла

. Итак, мы выяснили, что

.
На втором этапе исследуем, существует ли предел

.
Считая, что

малое по модулю отрицательное число, имеем:

При

предел первого сомножителя равен

, второго

, поэтому и

Найденный предел и есть число

. Это смещение (вернее, модуль

есть смещение).
Это уже означает, что асимптота существует. Остается в уравнение

подставить

и

. Получаем

И получается, что в уравнении асимптоты есть неизвестная
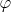
?
Это не неизвестная, а независимая переменная, с помощью которой в полярных координатах записываются уравнения кривых

. Такая же, как в Вашем уравнении

. Аналогичная независимой переменной

в декартовых.
Найдем уравнение асимптоты в декартовых координатах. Раскроем синус разности:

Так как

, то

