Предлагаю такую мысль. Мы знаем, что уравнение в производных выглядит, например, так:

Его можно воспринимать как условие на функцию

в какой-то точке

: мы вычисляем

и подставляем всё это в уравнение, и требуем, чтобы оно выполнялось. Не всякая функция подойдёт, даже та, которая принимает в этой точке нужное нам значение - нужно, оказывается, чтобы ещё и производная была подходящей, удовлетворяющей уравнению.
А теперь посмотрим на функцию как на график - то есть, на линию на плоскости

Когда мы утверждаем что-то про производную, то это "
тангенс-угла-наклона-касательной", то есть по сути, направление нашей линии. Как нам описать направление линии? Провести касательную, конечно же! Как нам описать касательную? Задать уравнение прямой! Вот так берём, и задаём:

... стоп.

и

- это координаты точки, через которую проходит наша
кривая линия. Если мы будем использовать их и для того, и для другого, то запутаемся. Представим себе уравнение типа
"

тот

который для кривой

тот

который для кривой

тот

который для касательной,

тот

который для кривой..."
Кошмар, правда? Нам нужно ввести
два набора символов: один набор, скажем,

относится только к кривой, а другой, скажем,

относится только к касательной. Тогда получается более внятно:

Окей?
По сути, именно это дифференциалы и делают. Только они идут ещё чуть дальше. Заметим, что касательная (она теперь описывается в переменных
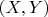
) всегда проходит через точку

поскольку в ней находится наша кривая, к которой эта касательная построена:

Это однозначно фиксирует одну из наших функций, выражает её через остальные:

И наше уравнение приобретает вид:

И чтобы не таскать это всё время за собой, вводят немного другие обозначения:

И окончательно уравнение приобретает вид:

Вот и всё. Теперь очевидно, что

и в то же время можно оперировать

и

как простыми удобными переменными. Делить, умножать, и превращать уравнения в дифференциалах в уравнения с производными и обратно.