1=0, а почему бы и нет?

[MestnyBomzh]

Вот полный текст доказательства того, что $1=0$, попутно доказывается тот факт, что все треугольники равносторонние

Рисунок:

Рассмотрим произвольный $\Delta ABC$. Проведем биссектрису угла $B$ и серединный перпендикуляр к стороне (середина $AC$ - точка $D$) $AC$; Точку их пересечения назовем $O$. Опустим из неё перпендикуляры $EO$ и $OF$ соответственно.
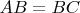
Так как $BO$ - биссектриса, то, из равенства $\Delta EBO$ и $\Delta OBF$ следует равенство $EB=BF$; Так как $DO$ одновременно и высота, и медиана $\Delta AOC$, то он равнобедренный и $AO=OC$. Значит прямоугольные треугольники $AEO$ и $OFC$ равны (из-за равенства $EO=OF$ и равенства гипотенуз) Значит $AE=FC$ Итого: $AB=BC$. Аналогично рассуждая для другой стороны докажем, что всякий треугольник равносторонний. Рассмотрим прямоугольный треугольник. Как было доказано ранее, он равносторонний, а значит все его стороны равны $a$. По теореме Пифагора: $2a^2=a^2$, значит $2=1$, вычитая единицу из последнего равенства получаем: $1=0$, что и требовалось доказать.

Я думаю, что форумчане легко найдут подвох:) Как по мне красивое доказательство, без всяких "скрытых" делений на ноль. Так вот, неужели $0\neq 1$ определило где пересекутся биссектриса и серединный перпендикуляр? Казалось бы, две совершенно не относящиеся друг к другу вещи, а как получилось то!

[provincialka]

Подвох действительно красивый. А вот что касается $1=0$, это притянуто за уши. Вроде как в "доказательстве" Бертрана Рассела.

[MestnyBomzh]

Почему притянутое? Если предположить, что $1=0$, прибавить к левой и правой частям уравнения $1$: $2=1$, домножить на любое $a^2\neq 0$, то по сути получим верное равенство же.

[gris]

Место пересечения биссектрисы и серединного перпендикуляра определяется свойством биссектрисы делить сторону проведения пропорционально боковым сторонам и иметь тупой угол напротив большей боковой стороны.

[provincialka]

Или просто тем, что они пересекаются на описанной окружности.

[gris]

Для меня это дело знакомо на практике.
Приходилось строить биссектрисы в огромном количестве. Ничего точнее и проще пропорционального деления стороны не придумалось

[migmit]

Ну вот, теперь мне мучительно долго вспоминать, у кого я это видел. Кажется, у Гарднера. Но может, и у Кэррола.

[nnosipov]

Этот софизм есть и подробно разобран в брошюре: Дубнов, Ошибки в геометрических доказательствах (серия "Популярные лекции по математике", вып. 11, М., 1961), пример 6 на стр. 14.

[migmit]

nnosipov в сообщении #814580 писал(а):

Этот софизм есть и подробно разобран в брошюре: Дубнов, Ошибки в геометрических доказательствах (серия "Популярные лекции по математике", вып. 11, М., 1961), пример 6 на стр. 14.

Блин, точно. Спасибо. Там и видел. Почему мне Г и К пригрезились?

[arseniiv]

Или у Пойа.

[MestnyBomzh]

nnosipov в сообщении #814580 писал(а):

Этот софизм есть и подробно разобран в брошюре: Дубнов, Ошибки в геометрических доказательствах (серия "Популярные лекции по математике", вып. 11, М., 1961), пример 6 на стр. 14.

Спасибо! С большим удовольствием прочёл доказательства для "других случаев"!)

[sergey1]

migmit в сообщении #814596 писал(а):

nnosipov в сообщении #814580 писал(а):

Этот софизм есть и подробно разобран в брошюре: Дубнов, Ошибки в геометрических доказательствах (серия "Популярные лекции по математике", вып. 11, М., 1961), пример 6 на стр. 14.

Блин, точно. Спасибо. Там и видел. Почему мне Г и К пригрезились?

Есть и у Гарднера в книге "Крестики-нолики" глава Геометрические заблуждения.