Подскажите верное направление в решении задачи. Вот условие:
Определить плотность распределения порядковой статистики

, если выборка

соответствует равномерному закону

.
Начало у меня такое:
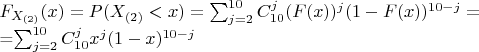
Так как у нас найдена функция распределения, а нам нужна плотность, то следует (?) продифференцировать функцию распределения

Всё ли верно, и что делать дальше?