Нужно показать, что следующий интеграл ограничен произведением константы на

.


- тензор четвертого порядка, симметричный, также выполняется


- линеаризованный тензор деформации,

Также выполняется уравнение.
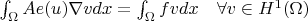
.

Что я могу.
Я знаю, как показать ограниченность для

:

Можно ли, используя это, каким-то образом доказать то, что требуется?
Можно ли, например, утверждать, что

для некоторого

, а потом определить взаимосвязь норм

и

?