Не хочу искать в литературе
Мда.
Вот посмотрите на это требование: должен существовать изоморфизм
Цитата:
Оно, если вдуматься, само по себе достаточно глупое. Слева и справа стоят просто множества, без всяких дополнительных структур. Два множества изоморфны тогда и только тогда, когда они просто-напросто равномощны. Ну, мало ли когда эти множества равномощны — например, оказалось, что они случайно оба счетны. Определение сопряженного функтора все-таки требует, чтобы эти изоморфизмы для каждой пары

были не какими попало, а
согласованными с морфизмами. Дело в том, что если заменить

на

посредством морфизма

в первой категории, то возникнет (по определению функтора) морфизм

, а отсюда (по функториальности
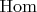
) — морфизмы

и

. Определение сопряженности говорит не только то, что между левыми частями этих морфизмов есть изоморфизм, и между правыми частями этих морфизмов есть изоморфизм, но и что они согласованны, то есть, переходят друг в друга посредством указанных морфизмов. Нарисуйте диаграмму из этих четырех
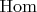
-ов — она должна быть коммутативной. Аналогичное происходит при замене

(с поправкой на ковариантность
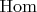
по второму аргументу.