Всем привет.
В общем в институте запарился с одним пунктом из работы, не могу сам разобраться, поскольку преподавателя тяжело отловить. Если кто-то поможет разобраться и сделать - буду очень благодарен. Я уже 2 дня не могу разобраться.
Итак.
Есть две исходные независимые выборки
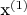
,
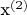
,
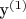
,
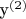
, соответственно, иксы - входные воздействия (факторы), игрики выходные (отклики).
Работая, большая, но вызвал проблему последний пункт:
1. В области изменения факторов
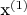
и
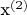
, то есть
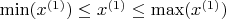
,
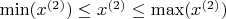
, выбрать исходную точку
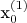
,
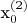
(нулевой уровень).
2. Выбрать шаги варьирования факторов (
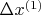
и
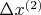
), провести полный факторный эксперимент 1-го порядка, определить коэффициенты регрессии
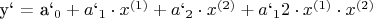
3. Осуществить просмотр факторного пространства по направлению оценок градиента функции y` по координатам
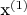
и
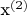
.
4. Выявить область, подозрительную на экстремум.
5. Принять координаты точки, в которой обеспечивается экстремум функции на найденном направлении, за нулевой уровень и повторить эксперимент.
6. Сделать выводы о характере поверхности отклика и о расположении экстремума функции y.
7. Если по результатам выполнения 1-5 нельзя сделать вывод о характере поверхности отклика и о нахождении экстремума функции y, необходимо повторить 1-5, выбрав другую исходную точку.
Формулы:
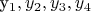
- По идее 4 точки вокруг выбранной (
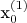
,
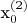
) на расстоянии от нее 10% расстояния от оси. Нахожу через:
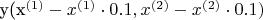
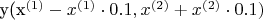
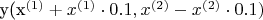
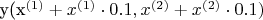
,
где y - функция, аппроксимирующая исходные данные (
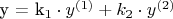
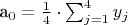
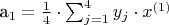
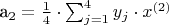
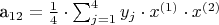
,
где
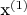
|
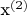
-1 | -1
-1 | +1
+1 | -1
+1 | +1
, ибо полный факторный эксперимент.
Шаги:
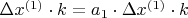
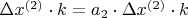
Уф, с теорией все. Теперь, что я делаю:
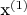
|
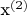
0.55 | 12.8
0.70 | 11.2
0.95 | 6.4
0.65 | 0.8
0.25 | 4.0
0.30 | 14.4
0.20 | 16.0
0.75 | 8.8
0.85 | 2.4
1.00 | 10.4
0.60 | 3.2
0.05 | 15.2
0.10 | 9.6
0.90 | 5.6
0.40 | 12.0
0.15 | 4.8
0.50 | 13.6
0.35 | 1.6
0.45 | 7.2
0.80 | 3.2
Аппроксимирующая функция:
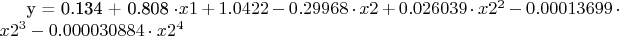
Выбираю точку
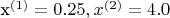
:
(Скрипт на Пайтоне по формулам выше)
Код:
Enter x1: .25
Enter x2: 4
Points around (0.25, 4.0):
Y (0.225, 3.6) = 0.605038708506
Y (0.225, 4.4) = 0.520278064154
Y (0.275, 3.6) = 0.645438708506
Y (0.275, 4.4) = 0.560678064154
In this point: a0 = 0.58285838633, a1 = 0.0202, a2 = -0.042380322176
Y` = 0.418387097626
Step /\x1` = a1(0.0202) * x1(0.25) * step(0.1) * k(1) = 0.000505
Step /\x2` = a2(-0.042380322176) * x2(4.0) * step(0.1) * k(1) = -0.0169521288704
С полученными шагами выполняю движение по осям, вычисляя на каждом шаге значение y, до тех пор, пока не выйдем за границы плоскости:
Код:
x1 = 0.25, x2 = 4.0, Y = 0.579430336
x1 = 0.250505, x2 = 3.98304787113, Y = 0.581638917442
x1 = 0.25101, x2 = 3.96609574226, Y = 0.583859834322
x1 = 0.251515, x2 = 3.94914361339, Y = 0.586093104996
x1 = 0.25202, x2 = 3.93219148452, Y = 0.588338747759
...
x1 = 0.333325, x2 = 1.20289873638, Y = 1.12241633752
x1 = 0.33383, x2 = 1.18594660751, Y = 1.12686362386
x1 = 0.334335, x2 = 1.16899447864, Y = 1.13132544618
x1 = 0.33484, x2 = 1.15204234977, Y = 1.13580181272
x1 = 0.335345, x2 = 1.1350902209, Y = 1.14029273169
x1 = 0.33585, x2 = 1.11813809203, Y = 1.14479821122
x1 = 0.336355, x2 = 1.10118596316, Y = 1.14931825937
x1 = 0.33686, x2 = 1.08423383429, Y = 1.15385288417
x1 = 0.337365, x2 = 1.06728170542, Y = 1.15840209356
x1 = 0.33787, x2 = 1.05032957655, Y = 1.16296589543
x1 = 0.338375, x2 = 1.03337744768, Y = 1.1675442976
x1 = 0.33888, x2 = 1.01642531881, Y = 1.17213730784
x1 = 0.339385, x2 = 0.999473189939, Y = 1.17674493387
x1 = 0.33989, x2 = 0.982521061069, Y = 1.18136718331
x1 = 0.340395, x2 = 0.965568932198, Y = 1.18600406376
x1 = 0.3409, x2 = 0.948616803328, Y = 1.19065558274
x1 = 0.341405, x2 = 0.931664674458, Y = 1.1953217477
x1 = 0.34191, x2 = 0.914712545587, Y = 1.20000256605
x1 = 0.342415, x2 = 0.897760416717, Y = 1.20469804512
x1 = 0.34292, x2 = 0.880808287846, Y = 1.20940819218
x1 = 0.343425, x2 = 0.863856158976, Y = 1.21413301447
x1 = 0.34393, x2 = 0.846904030106, Y = 1.21887251912
x1 = 0.344435, x2 = 0.829951901235, Y = 1.22362671323
x1 = 0.34494, x2 = 0.812999772365, Y = 1.22839560383
В общем, с этого момента я не понимаю ничего. Локальных экстремумов не видать, только увеличение значений, что делать не знаю. В общем, помогите, пожалуйста.