Здравствуйте, уважаемые форумчане!
Есть такая задачка: Вычислить объем тела, заданного ограничивающими его поверхностями:

,

Тело ограничено параболоидом и плоскостью. Не могу понять, как найти уравнение проекции данного тела на плоскость

, если приравнять

и упростить, то получится
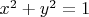
- а это вроде не есть искомая проекция.
Подскажите, пожалуйста.