Случайные велечины

[Creimi69]

Случайные величины $X$ и $Y$ независимы и имеют показательное распределение с параметром $\lambda=1$. Найти $M[X-Y], D[X-2Y]$, плотность распределения случайного вектора $(X,Y)$
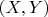
как я разобрался то $M[X-Y]=M[X]-M[Y]$, так как $M[X]=1/\lambda=1/1=1$ и $M[Y]=1/\lambda=1/1=1$, то из этого следует, что $M[X-Y]=M[X]-M[Y]=1-1=0$
$D[X-2Y]=D[X]-D[2Y]$, так как $D[X]=1/(\lambda^2)=1/1=1$ и $D[Y]=1/(\lambda^2)=1/1=1$, то из этого следует, что $D[X-2Y]=D[X]-D[2Y]=1-2=-1$
Я правильно сделал???
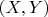
А вот как найти плотность распределения случайного вектора $(X,Y)$ я не знаю. от какой формулы отталкиваться??

[--mS--]

Нет. Правильно будет сначала прочесть и понять учебник, потом решать задачи. А не наоборот.

1. Приведите свойства дисперсии, какие знаете.

2. Приведите все известные Вам определения независимости случайных величин.

[Toucan]

Creimi69, замечание за дублирование темы, помещенной в Карантин. Дубль удален.