Здравствуйте!
Столкнулась с проблемой при самом начале решения(
Дана ф-я плотности

, определенная на промежутке: x принадлежит
![$[0;1]$ $[0;1]$](https://dxdy-03.korotkov.co.uk/f/2/1/a/21ad730ee7df0b97abd700cb0f8426e682.png)
,
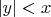
При других значениях

и

,

.
Найти с нужно через двойной интеграл

Но какие пределы интегрирования расставить? Для x понятно - от 0 до 1. А для

?
И как записать вероятность

,
можно ли через двойной интеграл - от 0 до

или тут по аналогии с одномерными функциями, нужно от единицы отнимать?
Пожалуйста, подскажите! Завтра сдавать....