Неявная схема для уравнения переноса.

[Firth]

Здравствуйте, помогите пожалуйста разобраться, что я делаю не так.
Используется разностная схема с центральной разностью для уравнения:

$$f_x+f_t=0$$

получается следующее:

$$\frac{f^{n+1}_{i+0.5}-f^n_{i+0.5}}{\tau}+\frac{f^{n+1}_{i+1.5}-f^{n+1}_{i-0.5}}{2h}=0$$

где $\tau$ -шаг по времени, а $h$ - шаг по сетке.
Далее положим $\frac{\tau}{h}=K$ и получим вот что

$$-0.5Kf_{i-0.5}^{n+1}+f_{i+0.5}^{n+1}+0.5Kf_{i+1.5}^{n+1}=f^n_{i+0.5}$$

Ну и формируется трех диагональная матрица

$$\begin{Vmatrix} 1 & 0.5K & 0 & 0 & 0 & \cdots & 0 & 0 & 0 \\ -0.5k & 1 & 0.5K & 0 & 0 & \cdots & 0 & 0 & 0 \\ 0 & -0.5K & 1 & 0.5K & 0 & \cdots & 0 & 0 & 0 \\ 0 & 0 & -0.5K & 1 & 0.5K & \cdots & 0 & 0 & 0 \\ \cdots & \cdots & \cdots & \cdots & \cdots & \cdots & \cdots & 0.5K & \cdots & \\ 0 & 0 & 0 & 0 & 0 & \cdots & -0.5K & 1 & 0.5K \\ 0 & 0 & 0 & 0 & 0 & \cdots & 0 & -0.5K & 1 \\ \end{Vmatrix} \begin{Vmatrix} f_{0.5}^n \\ f_{1.5}^n \\ f_{2.5}^n \\ f_{3.5}^n \\ \cdots \\ f_{N-1.5}^n \\ f_{N-0.5}^n \\ \end{Vmatrix}$$

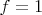
Замечательно, это мы можем решить с помощью метода прогонки. Условия следующие: на правой половине расчетной области в начальный момент времени $f=1$ а на левой $f=2$. $K=1$ тогда:

$$\begin{Vmatrix} 1 & 0.5 & 0 & 0 & 0 & \cdots & 0 & 0 & 0 \\ -0.5 & 1 & 0.5 & 0 & 0 & \cdots & 0 & 0 & 0 \\ 0 & -0.5 & 1 & 0.5 & 0 & \cdots & 0 & 0 & 0 \\ 0 & 0 & -0.5 & 1 & 0.5 & \cdots & 0 & 0 & 0 \\ \cdots & \cdots & \cdots & \cdots & \cdots & \cdots & \cdots & 0.5 & \cdots & \\ 0 & 0 & 0 & 0 & 0 & \cdots & -0.5 & 1 & 0.5 \\ 0 & 0 & 0 & 0 & 0 & \cdots & 0 & -0.5 & 1 \\ \end{Vmatrix} \begin{Vmatrix} 1\\ 1\\ 1\\ 1\\ \cdots \\ 2 \\ 2 \\ \end{Vmatrix}$$

Все верно? Правильно ли я мыслю? Конечно нет! Потому, что начинаю считать и получается полный бред. Где моя ошибка?