Интеграл от замкнутой 1-формы по кривым на рим. пов.

[Nimza]

Что можно сказать о замкнутой 1-форме $\omega$ на римановой поверхности $X$, если

$$ \int_\gamma \omega = 0 \; (\operatorname{mod} 2\pi) $$

для всех замкнутых кривых $\gamma$? Сразу видно, что значение интеграла постоянно на каждом гомотопическом классе кривых, а также на каждом классе одномерных сингулярных гомологий. Можно ли выписать явный вид такой формы? Хотя бы в случае компактных $X$.

-- Вт ноя 26, 2013 21:16:01 --

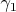
Нет, в компактном случае, вроде бы, неинтересно. Если обозначить за $\gamma_1$, $\ldots$, $\gamma_N$ замкнутые кривые, порождающие $H^s_1(M)$, а через $\omega_1$, $\ldots$, $\omega_N$ формы, порождающие $H^1_{dR}(M)$ с условием $\int_{\gamma_i} \omega_j = \delta_{ij}$, то выражая

$$ \omega = c_1 \omega_1 + \ldots + c_N \omega_N + df, $$

и подставляя в условие, получим

$$ \omega = 2\pi n_1 \omega_1 + \ldots + 2\pi n_N \omega_N + df, $$

где $n_k \in \mathbb Z$ (если я нигде не ошибся). А вот что делать в некомпактном случае?!

[Munin]

Как я понимаю, как-то так:

$$\begin{pmatrix}\text{замкнутая}\\\text{форма}\end{pmatrix}=\begin{pmatrix}\text{точная}\\\text{форма}\end{pmatrix}+\sum_{\text{по всем циклам}}\begin{pmatrix}\text{произвольный}\\\text{коэффициент}\end{pmatrix}\cdot\begin{pmatrix}\text{когомология для}\\\text{данного цикла}\end{pmatrix}$$

[Nimza]

Что Вы имеете в виду под "когомологией для данного цикла"?

[Oleg Zubelevich]

Munin

а я здесь, я далеко не уходил. сумма по всем циклам, это в смысле по всему континуму или сколько их там ? (первая часть марлизонского балета )

[Munin]

Nimza в сообщении #793114 писал(а):

Что Вы имеете в виду под "когомологией для данного цикла"?

У меня с терминологией бардак. Для одномерных сингулярных гомологий, являющихся образующими группы гомологий.

Nimza в сообщении #793054 писал(а):

А вот что делать в некомпактном случае?!

А в некомпактном ровно то же самое.