Порядковые типы

[Maximum]

Верно ли, что порядковые типы $\omega^{*}\cdot (\eta +2+\eta)$ и $\omega^{*}\cdot (\omega^{*}+2+\omega)$ совпадают?

Мне кажется, что совпадают. Как доказать? - Ясно, надо построить изоморфизм. Биекцию я еще как-то могу построить, но она у меня не сохраняет отношение! А может, я не прав, и они различны?

[Maximum]

А вот такое вот равенство верно: $\omega^{*}\cdot\omega^{*}=\omega^{*}\cdot\eta$ ?

[Maximum]

Кстати, $\omega^{*}$ - порядковый тип множества отрицательных целых чисел, $\eta$ - порядковый тип множества рациональных чисел.

[Someone]

Ага, это уже понятнее. А произведение в каком смысле? Определение нельзя здесь сформулировать?
Кстати, тогда $\omega^*+2+\omega$ - это порядковый тип множества целых чисел? А зачем там двойка?

[Maximum]

Понял. Сейчас все расскажу.

Пусть $A$ и $B$ - линейно упорядоченные множества. Множество $A$ называется подобным множеству $B$, если $A$ и $B$ изоморфны как частично упорядоченные множества.
Порядковым типом линейно упорядоченного множества $A$ называется класс всех линейно упорядоченных множеств, подобных $A$.
Будем считать 0 порядковым типом $\emptyset$. Через $n$ обозначим порядковый тип множества $\{0,1,\ldots,n-1\}$, где $0<1<\ldots<n-1,n\in\mathbb{N}$. Обозначим через $\omega,\omega^{*}$ и $\eta$ порядковые типы множеств натуральных, отрицательных целых(с порядком $\ldots<-2<-1$) и рациональных чисел соответственно.
Пусть дано семейство попарно попарно непересекающихся линейно упорядоченных множеств $A_{i}$ с порядковыми типами $\alpha_{i}$ и порядками
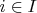
$\le_{i}$ соответственно, где $i\in I$, а $I$ линейно упорядочено отношением $\le_{I}$. Суммой порядковых типов $\alpha_{i}$ называется порядковый тип множества $\bigcup A_{i}$ c порядком $\le$, определенным следующим образом:

$$x\le y\Leftrightarrow (x,y\in A_{i} \text{ и } x\le_{i}y\text{ для некоторого }i\in I) \text{ или }(x\in A_{i_1},y\in A_{i_2}\text{ для некоторых }i_{1}\le_{I}i_{2}).$$

Пусть $\alpha$ и $\beta$ - порядковые типы линейно упорядоченных множеств $A$ и $B$ с порядками $\le_{A}$ и $\le_{B}$ соответственно. Произведением порядковых типов $\alpha$ и $\beta$ называется порядковый тип множества $A\times B$ с порядком $\le$, определенным следующим образом:

$$\langle x_{1},y_{1}\rangle\le\langle x_{2},y_{2}\rangle\Leftrightarrow( y_{1}\le_{B}y_{2})\text{ или }(y_{1}=y_{2}\text{ и }x_{1}\le_{A}x_{2}).$$

[Maximum]

То есть $\omega^{*}+2+\omega$ --- это множество, где сначала идут отр. числа,
потом множество, подобное {0,1}, и затем - натуральные числа {0,1,2,...} (тут 0 входит в $\mathbb{N}$). Порядок на этом множестве задается, как в определении.

[neo66]

Maximum писал(а):

А вот такое вот равенство верно: $\omega^{*}\cdot\omega^{*}=\omega^{*}\cdot\eta$ ?

Ну, слава богу! После того, как узнали определения можно начать разбираться с задачами.

Вышеуказанное равенство, конечно, неверно. Просто потому, что тип $\omega^{*}\cdot\omega^{*}$ имеет максимальный элемент $(-1,-1)$, а тип $\omega^{*}\cdot\eta$ не имеет.

Добавлено спустя 4 минуты 56 секунд:

Maximum писал(а):

То есть $\omega^{*}+2+\omega$ --- это множество, где сначала идут отр. числа,
потом множество, подобное {0,1}, и затем - натуральные числа {0,1,2,...} (тут 0 входит в $\mathbb{N}$). Порядок на этом множестве задается, как в определении.

Кстати, от того, входит $0$ в $\mathbb{N}$ или нет, этот порядковый тип не меняется. Кроме того, мне кажется, лучше обозначать натуральные числа с естественным порядком $\mathbb{N^+}$, поскольку $\mathbb{N}$ обычно резервируется за множеством целых чисел.

[Maximum]

Спасибо. Теперь если вернуться к исходной задаче, то у обоих множеств нет ни максимального, ни минимального элементов, поэтому они в принципе могут быть подобны. И почему-то мне кажется, что действительно эти порядковые типы совпадают. Но я не могу построить изоморфизм.

[neo66]

Maximum писал(а):

И почему-то мне кажется, что действительно эти порядковые типы совпадают.

Очень сильно сомневаюсь.

[Maximum]

Хм... Может, я поэтому не могу изоморфизм построить?
Ладно, значит, надо доказать, что они не совпадают. Дело ясное, от противного надо доказывать. Только вот в чем противоречие заключаться будет?

[neo66]

Maximum писал(а):

Верно ли, что порядковые типы $T_1=a\cdot b=\omega^{*}\cdot (\eta +2+\eta)$ и $T_2=a\cdot c=\omega^{*}\cdot (\omega^{*}+2+\omega)$ совпадают?

Во-первых, очевидно, $c=\omega^* + 2 + \omega = \mathbb{N}$.

Пусть биекция $f$, сохраняющая порядок, существует. Тогда она тем более сохраняет отношение непосредственного следования. Поэтому $\forall r \in b:f((-1,r)) = (-1,n)$ для некоторого $n$. Это ключевое наблюдение.
Рассмотрим $f^{-1}(-1,n-1)=(-1,r_1)$. И возьмем некоторое $r_2:$ $r_1<r_2<r$. Тогда $f((-1,r_2)$ будет иметь вид $(-k,n)$, $k\neq 1$, что невозможно.

[Maximum]

Огромнейшее спасибо!