Собственные значения и собственные векторы

[Мироника]

Дана матрица
-1 7 3
0 1 -2
0 1 4
Найти собственные значения и собственные векторы.
Собственные значения получились $\lambda_1=-1, \lambda_2=2, \lambda_3=3$
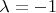
Начинаю искать собственные векторы при $\lambda=-1$ и получаю расширенную матрицу
0 7 3 0
0 2 -2 0
0 1 5 0
Преобразовывая ее получаю
0 7 3 0
0 0 1 0
0 0 0 0
Как же записать собственный вектор?

[Someone]

Эта матрица соответствует системе

$$\begin{cases}7x_2+3x_3=0\text{,}\\ \phantom{7x_2+3}x_3=0\text{.}\end{cases}$$

Из этой системы последовательно находим $x_3=0$, $x_2=0$, а $x_1$ находить неоткуда. Поэтому $x_1=t$, где $t\neq 0$ - любое число. Соответственно, собственный вектор

$$\vec a_1=\begin{pmatrix}t\\ 0\\ 0\end{pmatrix}=t\begin{pmatrix}1\\ 0\\ 0\end{pmatrix}\text{.}$$

Вместо $t$ можно взять любое число, не равное $0$.

[Мироника]

Нашла при $\lambda_1=-1$ собственный вектор $\alpha=(1,0,0)$,
при $\lambda_2=2$ собственный вектор $\beta=(-11,-6,3)$,
при $\lambda_3=3$ собственный вектор $\gamma=(-1,-1,1)$.
В задаче еще требуется сделать проверку. Что это значит?

[Brukvalub]

Мироника писал(а):

В задаче еще требуется сделать проверку. Что это значит?

Это значит - умножить вектор на матрицу (вектор - справа от матрицы) и убедиться, что в результате умножения получится вектор, пропорциональный исходному с коэф-том пропорциональности, равным собственному значению.

[Мироника]

Да, все получилось верно.
Спасибо!