Люди! Чувствую себя тормозом

3 Дня сижу, уже сил нету. Задача: необходимо построить кубическую параболу по двум точкам исходной функции, для которых известны значения f-ии в них и значения производной f-ии.
По сути, все данные для системы даны:
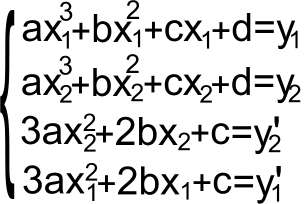
только, вот, решить я её не могу,

. Помогите, пожалуйста, мне для реализации метода нужно, из-за этого вся работа стоит....[/math]