Положим

По идее, надо доказать, что для

семейство функций

сходится к пределу по норме

.
Ну в самом деле. Из оценок на гладких функциях вытекает, что это семейство ограничено, а значит из него можно выбрать некую последовательность, слабо-сходящуюся к некоторому пределу

. Легко видеть, что этот предел как раз и совпадает с нашим оператором, определенным по непрерывности (умножаем на гладкие пробные функции, перебрасываем на них оператор и переходим к пределу).
Покажем, что и все семейство сходится к этой же функции, причем по норме

. Пусть это не так. Выбираем подпоследовательность

таких, что

. Это возможно с неким
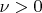
, поскольку по предположению сильной сходимости нет.
Теперь приближаем

гладкой функцией с ошибкой достаточно малой (в зависимости от

). Применяем оценки для этой гладкой функции, оцениваем ошибки и получаем противоречие.
Как-то так.