Облако точек

[l0l]

Добрый день уважаемые форумчане!
Затрудняюсь в решении следующей задачи:
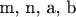
Имеется упорядоченное облако точек. Число горизонтальных рядов точек - m, число точек в ряде - n; шаг рядов - a, шаг точек в ряде - b. Параметры - m, n, a, b могут меняться, но m и n всегда $\ge$ 2, параметры a, b > 0.
Требуется найти сумму квадратов расстояний от каждой точки до центра этого поля: \sum $L_1^2 + $L_2^2 ... + $L_{mn}^2
Пробую алгоритм составить в MathCad но пока без результатно. Для наглядности привожу схемку.
Спасибо!

[San1990]

А зачем алгоритм, как по мне можно простую формулу вывести:
$ L_i^2 = ( i \mod n - 1)^2 b^2 / 4 + ( i \mod m - 1)^2 a^2 / 4 $
Получиться много однаковых слагаемых.

Например для верхнего ряда эта часть
$( i \mod m - 1)^2 a^2 / 4 $
будет общая

[nnosipov]

А Вы сначала формулу напишите для этой суммы квадратов. Здесь нужно будет рассмотреть случаи в зависимости от чётности $m$ и $n$ (от этого зависят координаты центра). Это нетрудно.

P.S. Да никаких случаев даже не надо рассматривать.

[l0l]

Дак вроде координата центра определяется достаточно просто, по вертикали $\frac{(m-1)a}{2}$
по горизонтали $\frac{(n-1)b}{2}$.
Проблема именно в создании алгоритма...

[nnosipov]

l0l в сообщении #778055 писал(а):

Проблема именно в создании алгоритма...

Какой алгоритм? Просто сумму вычислите, она легко считается (упражнение для школьников).

[l0l]

Не пойму... найти сумму для конкретного числа точек, например при m=4 и n=4 и известных шагах - не проблема. Но число рядов (m) и количество точек в ряде (n) может меняться. Я и пытаюсь составить алгоритм...

[nnosipov]

l0l в сообщении #778066 писал(а):

Но число рядов (m) и количество точек в ряде (n) может меняться.

Пусть себе меняется. Вы можете найти сумму членов произвольной конечной арифметической прогрессии? (Если нет, имеет смысл заглянуть в школьный учебник.) Ваша задача ненамного сложнее.