Решение систем ОДУ при большом N, случайное блуждание

[R_e_n]

Добрый день. Столкнулся с такой проблемой: есть система однородных дифференциальных уравнений первого порядка, вида:
${y_{i,j}(t)}'=a \cdot y_{i,j}(t)+b \cdot y_{i-1,j}(t)+c \cdot y_{i,j-1}(t)+d \cdot y_{i+1,j}(t)+e \cdot y_{i,j+1}(t)$
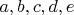
где $a, b, c, d, e$ - известные константы; $i,j=1,...,n$ Известны так же начальные значения $y_{i,j}(0)$

Нужно найти все $y_{i,j}(t)$ проблема в том, что $n=40$ уравнений будет 1600.

Для решение системы ОДУ составляется характеристическое уравнение ищутся его корни и т. д. но тут такая большая размерность, как быть?

Может есть какой-нибудь удобный сервис для решения таких систем, которое справится с этим?