Изменение сложности алгоритма от природы переменной

[DmitryKober]

Доброго времени суток!

Я новичок в оценке алгоритмов и хотел бы разобраться что к чему. Пусть есть код, написанный на Java:

for (int i = 1; i < k; i++) {
   for (int j = (n-k)/(k-1); j >= 0; j=j-2) {
      List<Task> tasks = new ArrayList<Task>();
      initTheList(tasks, j); // fills the list with j tasks
      someFunction(tasks);
   }
}

private void someFunction(List<Task> tasks) {
   ...
   Collections.sort(tasks, new ConstantTimeComparator());
   ...
}

Как видите, тут 2 цикла: внутренний и внешний. Во внутреннем цикле создается список объектов Task и заполняется этими объектами случайно. Важно, что длина этого списка равна $j$. Кроме того, во внутреннем цикле присутствует функция someFunction(), самой трудоемкой (и важной) частью которой является сортировка (по умолчанию в Java применяется сортировка слиянием), вычислительная сложность которой $O(g_i \cdot (\log{g_i}))$, где $g_i$ - размер входного массива.

1) Верно ли, что если $k = \frac{n}{b}$, где $b$ - некоторая константа, то общая вычислительная сложность алгоритма равна $O(n)$?
Я рассуждал так: раз $k$ выражается через $n$, то выражение $O(\frac{n-k}{k-1}\cdot\log{\frac{n-k}{k-1}})$ равно $O(1)$, аналогично, внутренний цикл даст $O(1)$, и, наконец, внешний цикл даст $O(k) = O(n)$

2) Верно ли, что если $k$ - константа, то общая сложность алгоритма - $O(n^2 \cdot \log{f})$, где $f = \frac{n-k}{k-1} $
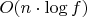
Рассуждение такое: внешний цикл даст $O(1)$, внутренний цикл - $O(n)$, а функция someFunction() даст $O(n \cdot \log{f})$, где $f = \frac{n-k}{k-1} $.

Не могли бы вы проверить рассуждения, и, если неправильно, объяснить где ошибка, и как правильно нужно было вести рассуждение? Заранее спасибо.

[Pavia]

1) Верно
2) Не верно. В ответе не должно быть констант, в частности k.

Может я придираюсь, но не плохо бы учесть при решение что деление в коде целочисленное. А в решение оно у вас сразу указывается дробным.

[DmitryKober]

Pavia, большое спасибо за ответ!

Тогда получается, что во втором случае ответ просто $O(n^2 \cdot \log{n})$?

Если честно, я не понял, что Вы имели ввиду на счет целочисленного деления. Не могли бы Вы уточнить?