Mikhail Sokolov писал(а):
другой несмещенной оценки для суммы
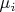
-ых, по-мойму, просто нет.
Приведу более простой пример. Существут две альтернативы:

и

. Про вероятности ничего не известно. В единственном испытании

произошло. Можно ли сделать какие-то оценки вероятности

?
Если принять некие исходные гипотезы, то можно. Например, можно принять гипотезу, что априорное распределение параметра

равномерное по отрезку
![$[0,1]$ $[0,1]$](https://dxdy-03.korotkov.co.uk/f/a/c/f/acf5ce819219b95070be2dbeb8a671e982.png)
. По формуле Байеса нетрудно получить плотность апостериорного распределения параметра

:

(исходя из того, что

)
Как теперь перейти от этого распределения к точечной оценке

? Здесь возможны разные варианты. Оценка по максимуму вероятности даст

(для нескольких испытаний - отношение количества положительных исходов к количеству испытаний:

). Оценка по мат. ожиданию (средне-вероятная) даст

(для нескольких испытаний:

).
Как видите, точечные оценки могут быть разными даже при одинаковых априорных предположениях.