Здравствуйте. Разбираюсь с логикой и дискретной математикой, пока совсем не выходит, чувствую, что нужна помощь.
Задача. Пусть

и

- отображения, и

Докажите, что

- инъекция, а

- сюръекция.
Во-первых, запутался в понятиях. Тождественное отображение - функция переводит аргумент в себя.
Как это связать с "обратностью"?

, но если

- обратная функция для

, то они взаимно однозначны, и это биекция?
И если

- обратная к

, то

и

Далее: пусть

,

Если

- инъективна, то

. Если при этом

тоже инъективна, то для


, что возможно только если
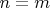
Если же

- сюръективна, то для

, что верно, учитывая инъективность

.
Чувствую, что написал полный бред, тем более, что у меня получается и обратное:

- сюръективна,

- инъективна.
Вообще мало что понимаю, хотя прочитал много всего на тему.