В исходном уравнение без потери общности можно считать, что

и

. Само же уравнение эквивалентно:

Отсюда следует, что

делит
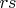
,

делит
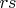
, а значит и

делит
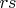
. Но аналогично можно получить, что
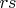
делит

. С необходимостью имеем

, а уравнение преобразуется к виду:

где

,

.
С помощью мапла получаем, что последнее уравнение эквивалентно элиптической кривой:

Отсюда для каждого значения

можно проверить, представимо ли оно в искомом виде.
-- Fri Sep 06, 2013 09:26:20 --Пример.

представимо в указанном виде с

Если ли меньшее представление, не проверял. Но различных представлений для

бесконечно много, так как ранг кривой здесь равен 1.