Существуют ли такие натуральные числа

и

, что уравнение

Имеет более одного положительного вещественного корня?
(внутривтузовский тур)Мне кажется, что нет.
При

наша башня всегда

, а дробь, наоборот,

.
Если же
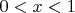
, то башня

, а дробь

.
Так что, при любых

имеем единственный положительный вещественный корень

.
Только я понятия не имею, как всё это доказывать.