TelmanStudЯ, возможно, не поняла Вашей проблемы. Вы хотите научиться понимать эту картинку? или ее строить?
Если первое, то
Munin правильно все понял, точки одного цвета (яркость не берется в расчет) - это точки с одним аргументом. Чем больше модуль, тем меньше яркость, вблизи нуля точки с фиксированным аргументом имеют самый насыщенный цвет. Нули функции отображаются черным. Полюса - белым.
Карта цветов - следующая:

Здесь по горизонтали - вещественная ось, по вертикали - мнимая. Видно, что точки с одним аргументом покрашены в один цвет.
А вот "график"

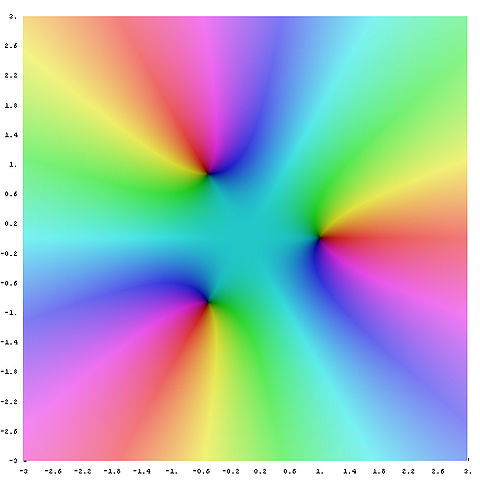
Откуда общее впечатление: есть три нуля (что верно), три точки с одинаковыми кубами при

и что-то непонятное происходит при

. Что? Такое ощущение, что у большей части этих точек аргумент

близок к

. Ну, в общем, чем модуль

ближе к нулю, тем этот аргумент ближе к

, так и есть. А в целом на круге фигурина будет замысловатая, посчитать можно, но и из картинки видно. Иначе зачем ее строить.
Ту ссылку я Вам дала, потому что там можно параллельно строить, как выглядят 3D графики аргумента и модуля, вещественной части и мнимой части... кому как, для меня это нагляднее.