Показательное уравнение

[ain1984]

Уважаемые участники форума!

Помогите, пожалуйста, разобраться со следующим уравнением:

$$13^{2x}-6\cdot13^x+5=0$$

Моё решение:

Сделаем замену: $13^x=t$, тогда:

$$t^2-6t+5=0$$

Решая данное уравнение, находим два корня: $t_1=5$, $t_2=-1$.

$$13^x=5 \qquad 13^x=-1$$

Второе уравнение не имеет корней.
Решая первое, находим корень:

$$x=\log_{13}5$$

Но данное уравнение имеет ещё один корень: $x=0$. Действительно,

$$13^0-6\cdot13^0+5=0$$

$$1-6+5=0$$

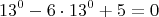
Но как его получить, я не понимаю. Подскажите, пожалуйста.

[nnosipov]

ain1984 в сообщении #745674 писал(а):

Решая данное уравнение, находим два корня: $t_1=5$, $t_2=-1$.

Будьте внимательней при решении квадратных уравнений. Чему на самом деле равен $t_2$?

[ain1984]

nnosipov, спасибо. Конечно, я тут ошибся. $t_2=1$.