Sylvester's construction

[galaxy]

В Википедии пишут, что построение матриц Адамара вида
$H_1 = \begin{bmatrix} 1 \end{bmatrix}, $
$H_2 = \begin{bmatrix} 1 & 1 \\ 1 & -1 \end{bmatrix}, $
$H_{2^k} = \begin{bmatrix} H_{2^{k-1}} & H_{2^{k-1}}\\ H_{2^{k-1}} & -H_{2^{k-1}}\end{bmatrix}$
называется Sylvester's construction (кстати, как правильно перевести?) и дается ссылка на статью J.J. Sylvester. Thoughts on inverse orthogonal matrices, simultaneous sign successions, and tessellated pavements in two or more colours, with applications to Newton's rule, ornamental tile-work, and the theory of numbers. Philosophical Magazine, 34:461–475, 1867.
Я скачал эту статью, но я не очень силен ни в английском, ни в математике. Пролистал её много раз и вчитывался в фрагменты, но ничего похожего на такое построение не нашел. Лишь в конце что-то похожее на матрицу Уолша. Еще заметил, что это только первая часть статьи. В конце написано "Part II. to follow". Может, то, что меня интересует находится во второй части? (и была ли вообще опубликована вторая часть статьи?) В ссылке указаны номера страниц 461–475 и это как раз то, что у меня есть.

И еще вопрос. Термин Sylvester's construction применим только к матрицам Адамара? Например, если я напишу построение матрицы сложения (суммы индексов элементов):
$A_1 = \begin{bmatrix} 0 \end{bmatrix}, $
$A_2 = \begin{bmatrix} 0 & 1 \\ 1 & 2 \end{bmatrix}, $
$A_{2^k} = \begin{bmatrix} A_{2^{k-1}} & A_{2^{k-1}} + 2^{k-1}J_{2^{k-1}}\\ A_{2^{k-1}} + 2^{k-1}J_{2^{k-1}} & A_{2^{k-1}} + 2^{k}J_{2^{k-1}}\end{bmatrix}, $ где $J_n$ — матрица единиц.
То это будет Sylvester's construction или просто рекуррентное построение матриц?

P.S. Я немного изучаю подобные построения и собираюсь кое-что опубликовать по этой теме в сети, поэтому мне хотелось бы прояснить эти вопросы.

[Xaositect]

galaxy в сообщении #742817 писал(а):

Sylvester's construction (кстати, как правильно перевести?)

Конструкция Сильвестра. Это не термин, просто есть некоторый способ построения ортогональных матриц, который придумал Сильвестр.

galaxy в сообщении #742817 писал(а):

Я скачал эту статью, но я не очень силен ни в английском, ни в математике. Пролистал её много раз и вчитывался в фрагменты, но ничего похожего на такое построение не нашел.

Пункт 6

Цитата:

6. (1) I observe that there will be as many distinct types of solutions as there are dislinct modes of breaking $n$ into factors*.

(2)Let $n = p . q . r \dots$ be one of the decompositions in question. Write down the disjunctive product

$$(1, a, a^2 , \dots a^{p-1} \between 1, b, b^2 , \dots b^{q - 1} \between 1, c, c^2 , \dots c^{r -1} \between \dots\phantom)$$

in which the terms are to follow any fixed law of succession. This will produce a line containing $p . q . r \dots$, i. e. $n$ terms.
Let $a, b, c, \dots$ respectively represent the $p$th, $q$th, $r$th, … roots of unity; by giving to each of these quantities successively its $p$, $q$, $r$, … values we shall obtain $p . q . r \dots$, i. e. $n$ lines, constituting a matrix of the $n$th order; the totality of the matrices so formed contain between them the complete solution of the $(n - 1)^2$ system of equations.

Перевод, примечания мои:

Цитата:

6. (1) Покажем, что существует столько же типов решений [До этого Сильвестр говорит, что элементы обратно-ортогональной (inverse orthogonal) матрицы порядка $n$ должны удовлетворять системе из $(n-1)^2$ независимых уравнений], сколько существует способов разложения $n$ на множители.

(2) Пусть $n = p\cdot q\cdot r\dots$ --- одно из таких разложений. Запишем дизъюнктивное произведение [Имеется в виду строка, содержащая все возможные произведения элементов, взятых по одному из каждой скобки. В современной терминологии - тензорное произведение строк]

$$(1, a, a^2 , \dots a^{p-1} )\otimes (1, b, b^2 , \dots b^{q - 1}) \otimes (1, c, c^2 , \dots c^{r -1}) \otimes \dots,$$

в котором фиксирован некоторый порядок сомножителей. Получим строку, содержащую $p\cdot q\cdot r\dots$, т.е. $n$ элементов.
Пусть $a, b, c\dots$ означают корни из единицы соответственно $p$-й, $q$-й, $r$-й … степени; перебирая последовательно $p$, $q$, $r$ … значений этих корней мы получим $p\cdot q\cdot r\dots$, т.е. $n$ строк, составляющих матрицу порядка $n$; множество всех образованных таким образом матриц содержит все решения системы $(n-1)^2$ уравнений [имеется в виду, что любую ортогональную матрицу можно получить из такой матрицы с помощью конструкции, описанной в п. 4]

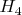
Матрицы Адамара получаются из этой конструкции в случае, когда рассматривается разложение $2^k = 2\cdot 2\cdot 2\dots\cdot 2$. Например, из двух матриц, построенных для $n = 4$ вторая является матрицей Адамара $H_4$ в Ваших обозначениях.

galaxy в сообщении #742817 писал(а):

То это будет Sylvester's construction или просто рекуррентное построение матриц?

Нет, это не конструкция Сильвестра.

[galaxy]

Спасибо. Разобрался с конструкцией Сильвестра из статьи.

Xaositect в сообщении #742833 писал(а):

Матрицы Адамара получаются из этой конструкции в случае, когда рассматривается разложение $2^k = 2\cdot 2\cdot 2\dots\cdot 2$. Например, из двух матриц, построенных для $n = 4$ вторая является матрицей Адамара $H_4$ в Ваших обозначениях.

Только вопрос в том, что первая матрица не выражается через конструкцию Сильвестра из вики. Тем более, что конструкция из вики дает только одну матрицу заданного размера, а при конструкции из статьи с увеличением размера, количество получаемых матриц растет комбинаторно. Следовательно, конструкция Сильвестра из вики не является эквивалентом конструкции Сильвестра из статьи. Как это объяснить?

[Xaositect]

galaxy в сообщении #742886 писал(а):

Только вопрос в том, что первая матрица не выражается через конструкцию Сильвестра из вики. Тем более, что конструкция из вики дает только одну матрицу заданного размера, а при конструкции из статьи с увеличением размера, количество получаемых матриц растет комбинаторно. Следовательно, конструкция Сильвестра из вики не является эквивалентом конструкции Сильвестра из статьи. Как это объяснить?

Сильвестр рассматривает не матрицы Адамара, а обладающие более общим свойством - обратно-ортогональные (inverse orthogonal). Матрицы Адамара - это обратно-ортогональные матрицы, состоящие из единиц и минус единиц. Первая матрица не является матрицей Адамара.

[galaxy]

Про то, что написано в статье Сильвестра я с вами согласен.

Wikipedia в Hadamard matrix писал(а):

In this manner, Sylvester constructed Hadamard matrices of order 2k for every non-negative integer k

Я хочу понять, что имеет в виду вики. На мой взгляд, в вики совсем другое построение, которое не имеет отношение к статье, хотя ссылка есть и вызывает вопрос.