Критерий оптимальности для случайных процессов

[sergeykondr]

Добрый день.

У меня возникла вот такая задача.

Существует случайный процесс Т $\lbrace X_t \rbrace t\in T$. Пусть имеются две величины $x_0, x_t$. Положим, что $x_t <x_0$. Величина $x_0$ является фиксированной точкой, так что $ \triangle x = x_0-x_t$ так же случайная величина.
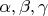
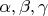
Так же, существует определенный критерий эффективности $\delta=\alpha - \frac {\beta}{\triangle x + \gamma}, \lbrace \triangle x \in \mathbb{N}, \triangle x \geqslant \frac{\beta}{\alpha} - \gamma\rbrace$, где $\alpha, \beta, \gamma$ известные параметры. Кроме того, существует неопределенный критерий $\tau=\omega \frac1t$, где $\omega$, в отличие от $\alpha, \beta, \gamma$ величина, зависимая от случайного процесса, в свою очередь неопределима по условию задачи.
Суть вопроса состоит в том, что бы найти критерий оптимальности, используя заданные функции и отыскать $\max\delta$ при конечном значении $\triangle x$.
Понятное дело, что можно ввести такую величину $\varepsilon$, что $1-\delta \leqslant \varepsilon $. Тогда очевидно, что $\varepsilon$ так же зависит от множества параметров $\lbrace P_i \rbrace $, зависимых от случайного процесса.
Существует ли какой-то универсальный критерий для такого рода сходимости, например квадрат функции или отношение величины к ее квадрату, похожими на те, которые применяют для классификации иррациональных чисел, представляя отношением рациональных чисел и разделяя их на диофантовы и лиувиллевы числа?

[profrotter]

Очень не аккуратно обращаетесь со словом "критерий". Везде, где Вы написали "критерий" никакого критерия не указано. Отсюда непонятно, что у вас там существует и что Вы хотите найти.

[sergeykondr]

profrotter в сообщении #741320 писал(а):

Очень не аккуратно обращаетесь со словом "критерий". Везде, где Вы написали "критерий" никакого критерия не указано. Отсюда непонятно, что у вас там существует и что Вы хотите найти.

Хорошее замечание! Заданы функции: $\delta(\triangle x, \alpha, \beta, \gamma), \tau(t, \omega)$. Необходимо найти критерий оптимальности общей целевой функции $C_{opt}(\delta, \tau)$, при котором $\delta$ будет оптимальным. Речь идет о том, что нужно $\max\delta(\triangle x)$ и $\min t$.
Спасибо! Мысли бегут впереди паровоза .