Пока в Вашей задаче нет ни задачи, ни серьёзных попыток решения. Методом максимального правдоподобия оценивают параметр(ы) распределения по некоторой выборке. Где она? Кто такое

- может, это её объём, так где она сама? Так и быть, я её Вам заведу, но решать Вы будете сами.
Итак, есть модель регрессии

. В результате

независимых наблюдений, в которых переменная

принимала неслучайные значения

, получены следующие отклики (значения зависимой переменной)

,

. Здесь
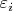
- независимые и одинаково распределённые случайные ошибки с плотностью распределения

.
Так или не так?
Во-первых, Вам следует выяснить, что это за плотность - какого распределения, сколько тут неизвестных параметров - то ли два (

и

), то ли меньше.
Дальше следует найти функцию правдоподобия вектора

, и по ней искать оценки неизвестных параметров. А не то, чем Вы выше занимались.