Господа, подскажите, откуда берется подобная формула?
Одношаговое предсказание распределения входящих звонков в момент времени, учитывая, что имеется информация о

, где

-кол-во входящих звонков в промежуток времени
![$(i-1;i]$ $(i-1;i]$](https://dxdy-01.korotkov.co.uk/f/8/8/c/88cf2f6e05f6c3fd5a4d9c787563c12d82.png)
.

- интенсивность поступления заявок.

где

~Пуассоновское

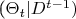
~Гамма
