Дьявольские магические квадраты из простых чисел

[Nataly-Mak]

О борьбе с дырками…

Покажу одно из преобразований «плюс-минус», сохраняющее магическую константу квадрата и его свойства идеального квадрата:

5651-z 761 3671 5273+z 173 2111 1607+z 5231 3011 2081-z
5351 977+z 5843-z 47 5003 2693 5657 1985-z 2003+z 11
653 2591 4217 4007 1223 53 3533 5393 2663 5237
1901 3203 4391 1913 4091 2153 3917 2063 3491 2447
941 4817 1493 4751 983 4463 1277 4943 1181 4721
1193 4733 971 4637 1451 4931 1163 4421 1097 4973
3467 2423 3851 1997 3761 1823 4001 1523 2711 4013
677 3251 521 2381 5861 4691 1907 1697 3323 5261
5903 3911-z 3929+z 257 3221 911 5867 71+z 4937-z 563
3833+z 2903 683 4307-z 3803 5741 641-z 2243 5153 263+z

Здесь z – любое целое число.

Пример
$z=10$
Применив преобразование при таком значении z, получим следующий идеальный квадрат:

5641 761 3671 5283 173 2111 1617 5231 3011 2071
5351 987 5833 47 5003 2693 5657 1975 2013 11
653 2591 4217 4007 1223 53 3533 5393 2663 5237
1901 3203 4391 1913 4091 2153 3917 2063 3491 2447
941 4817 1493 4751 983 4463 1277 4943 1181 4721
1193 4733 971 4637 1451 4931 1163 4421 1097 4973
3467 2423 3851 1997 3761 1823 4001 1523 2711 4013
677 3251 521 2381 5861 4691 1907 1697 3323 5261
5903 3901 3939 257 3221 911 5867 81 4927 563
3843 2903 683 4297 3803 5741 631 2243 5153 273

$K=5914, S=29570$

Ничего не могу сказать об эффективности данного преобразования в борьбе с дырками: слишком много изменяется элементов - 16 штук (пока не попробовала).
[Аналогичное преобразование испытывала в борьбе с дырками в пандиагональных квадратах 8-го порядка, там иногда удавалось ликвидировать одну-две дырки; в тех случаях в преобразовании участвовали только 8 элементов квадрата.]
Однако преобразование интересно само по себе.

-- Вт мар 03, 2015 09:17:32 --

Между тем программа у меня продолжает работать. Решений с 4 дырками находится довольно много (ниже несколько показано), с 6 дырками уже и не вывожу. А вот с 2 дырками пока не найдено ни одного решения.
Подумываю потихоньку, как бы оптимизировать программу. Шаблон использовать? У меня в этой программе шаблон не используется. Надо сделать шаблон по решению с 4 дырками - по самому близкому приближению к решению. Авось и полное решение найдётся по этому шаблону.

Решения с 4 дырками показываю, может, помогут кому-нибудь придумать, как эти решения довести до полных.
Совсем чуть-чуть остаётся, и никак

(Оффтоп)

2543 977 1223 5897 5483 5273 3011 3533 107 1523 
5717 1433 5237 1367 761 653 5393 4601 827 3581 
2693 2003 3233 4967 1907 683 5297 1787 3677 3323 
3701 53 5741 1913 4091 2153 3917 2063 3491 2447 
941 4817 1493 4751 983 4463 1277 4943 1181 4721 
1193 4733 971 4637 1451 4931 1163 4421 1097 4973 
3467 2423 3851 1997 3761 1823 4001 173 5861 2213 
2591 2237 4127 617 5231 4007 947 2681 3911 3221 
2333 5087 1313 521 5261 5153 4547 677 4481 197 
4391 5807 2381 2903 641 431 17 4691 4937 3371

2663 4691 4391 947 113 3371 1025 3011 5741 3617 
2591 911 5471 4139 3533 3833 4007 17 4937 131 
5051 4217 743 263 5717 617 1787 5867 4547 761 
431 5261 3803 1913 4091 2153 3917 2063 3491 2447 
941 4817 1493 4751 983 4463 1277 4943 1181 4721 
1193 4733 971 4637 1451 4931 1163 4421 1097 4973 
3467 2423 3851 1997 3761 1823 4001 2111 653 5483 
5153 1367 47 4127 5297 197 5651 5171 1697 863 
5783 977 5897 1907 2081 2381 1775 443 5003 3323 
2297 173 2903 4889 2543 5801 4967 1523 1223 3251 

683 4937 2381 5861 2081 4007 2213 5717 1433 257 
3677 47 3911 1799 5813 2657 4691 971 5897 107 
2663 4391 5843 911 443 131 3137 5171 4547 2333 
1901 2357 5237 1913 4091 2153 3917 2063 3491 2447 
941 4817 1493 4751 983 4463 1277 4943 1181 4721 
1193 4733 971 4637 1451 4931 1163 4421 1097 4973 
3467 2423 3851 1997 3761 1823 4001 677 3557 4013 
3581 1367 743 2777 5783 5471 5003 71 1523 3251 
5807 17 4943 1223 3257 101 4115 2003 5867 2237 
5657 4481 197 3701 1907 3833 53 3533 977 5231 

2237 4007 4013 521 4691 617 479 5531 3671 3803 
4937 2357 3701 863 4391 5897 2333 4421 563 107 
3911 131 5483 71 4127 5153 113 443 5657 4481 
3533 3251 2711 1913 4091 2153 3917 2063 3491 2447 
941 4817 1493 4751 983 4463 1277 4943 1181 4721 
1193 4733 971 4637 1451 4931 1163 4421 1097 4973 
3467 2423 3851 1997 3761 1823 4001 3203 2663 2381 
1433 257 5471 5801 761 1787 5843 431 5783 2003 
5807 5351 1493 3581 17 1523 5051 2213 3557 977 
2111 2243 383 5435 5297 1223 5393 1901 1907 3677 

2081 2111 3617 863 5003 3011 4547 2663 5657 17 
3221 5231 2591 2861 5741 3203 641 107 5903 71 
1223 5717 401 2237 2543 5531 2243 113 5651 3911 
3701 4007 1787 1913 4091 2153 3917 2063 3491 2447 
941 4817 1493 4751 983 4463 1277 4943 1181 4721 
1193 4733 971 4637 1451 4931 1163 4421 1097 4973 
3467 2423 3851 1997 3761 1823 4001 4127 1907 2213 
2003 263 5801 3671 383 3371 3677 5513 197 4691 
5843 11 5807 5273 2711 173 3053 3323 683 2693 
5897 257 3251 1367 2903 911 5051 2297 3803 3833 

911 3617 5483 1223 3323 5867 2333 101 3701 3011 
2243 743 3557 113 4007 3203 3251 2795 5531 4127 
4481 5807 1319 3221 5393 2111 443 5087 1697 11 
5741 617 3137 1913 4091 2153 3917 2063 3491 2447 
941 4817 1493 4751 983 4463 1277 4943 1181 4721 
1193 4733 971 4637 1451 4931 1163 4421 1097 4973 
3467 2423 3851 1997 3761 1823 4001 2777 5297 173 
5903 4217 827 5471 3803 521 2693 4595 107 1433 
1787 383 3119 2663 2711 1907 5801 2357 5171 3671 
2903 2213 5813 3581 47 2591 4691 431 2297 5003 

257 3617 1697 2357 5531 5351 4805 101 5237 617 
2243 5897 47 5843 683 1901 3251 1397 3221 5087 
3581 2213 5807 977 4691 2111 2591 3911 3677 11 
5861 263 3371 1913 4091 2153 3917 2063 3491 2447 
941 4817 1493 4751 983 4463 1277 4943 1181 4721 
1193 4733 971 4637 1451 4931 1163 4421 1097 4973 
3467 2423 3851 1997 3761 1823 4001 2543 5651 53 
5903 2237 2003 3323 3803 1223 4937 107 3701 2333 
827 2693 4517 2663 4013 5231 71 5867 17 3671 
5297 677 5813 1109 563 383 3557 4217 2297 5657

[Nataly-Mak]

Возвращаюсь к идеальным квадратам 9-го порядка.
Выше я рассказала о частной формуле таких квадратов, в которой всего 12 свободных переменных из 40.
Формулу реализовала, программу покрутила, пока ничего не нашла. Как я уже говорила, палка о двух концах. Уменьшение количества свободных переменных сокращает перебор, но сильно ограничивает пространство решений.
Найти решения, обладающие такими дополнительными свойствами, сложнее, нежели найти любой идеальный квадрат.

Поэтому получаю общую формулу идеальных квадратов 9-го порядка:

X(1) = (2*X(32)-2*X(34)+2*X(16)-2*X(18)- K+2*X(24)+2*X(8)-2*X(26)+2*X(40))/2 
X(11) = - X(32)- X(6)- X(34)+ X(35)-2*X(36)+2*X(10)- X(16)- X(12)-2*X(18)- X(7)+ X(20)-2*X(2) - X(22)+4*K- X(26)- X(27)+ X(28)- X(29)+2*X(30)+2*X(40) 
X(14) = - X(32)- X(6)- X(16)- X(12)- X(2)- X(22)+5*K- X(24)- X(8)- X(4) 
X(15) = 3*X(32)+3*X(6)+ X(34)- X(35)+3*X(36)-4*X(10)- X(13)+2*X(16)+2*X(12)+2*X(18)+2*X(7) -2*X(20)+4*X(2)+3*X(22)-9*K+ X(24)+2*X(8)+2*X(26)+2*X(27)- X(28) + X(29)-3*X(30)+ X(4)-3*X(40) 
X(17) = (-2*X(32)-2*X(6)-2*X(36)+2*X(10)-2*X(16)-2*X(12)-2*X(18)-2*X(7)+2*X(20) -2*X(2)-2*X(22)+9*K-2*X(8)-2*X(26)-2*X(27)+2*X(30)+2*X(40)) /2 
X(19) = -(-2*X(6)-4*X(34)+2*X(35)-4*X(36)+6*X(10)-6*X(18)-2*X(7)+4*X(20)+2*X(3) -2*X(2)-2*X(22)-3*K+2*X(24)+2*X(8)-4*X(26)-2*X(27)+4*X(28) -2*X(29)+4*X(30)+2*X(4)+6*X(40)) /2 
X(21) = 2*X(32)+2*X(6)- X(35)+ X(36)-2*X(10)- X(13)+2*X(16)+ X(12)+2*X(7)- X(20)+2*X(2)+ X(22) -4*K+ X(24)+2*X(8)-2*X(30)+ X(4)- X(40) 
X(23) = - X(32)- X(6)+ X(34)+ X(35)+ X(10)- X(16)- X(12)+ X(18)- X(7)- X(3)- X(2)- X(22)+3*K - X(24)- X(8)+ X(29)+ X(30)- X(4) 
X(25) = - X(32)-2*X(6)-3*X(34)+ X(35)-3*X(36)+4*X(10)+ X(13)- X(16)-4*X(18)-2*X(7)+2*X(20) +2*X(3)-2*X(2)-2*X(22)+4*K-3*X(26)-2*X(27)+2*X(28)-2*X(29) +3*X(30)+ X(4)+4*X(40) 
X(31) = X(32)+2*X(6)- X(35)+ X(36)-2*X(10)- X(13)+ X(16)+ X(12)+ X(18)+ X(7)- X(20)+2*X(2)+ X(22) -2*K+ X(24)+ X(8)+ X(26)+ X(27)- X(28)-2*X(30)-2*X(40) 
X(33) = (-4*X(32)-4*X(6)-2*X(34)-4*X(36)+4*X(10)+2*X(13)-2*X(16)-2*X(12)-2*X(18)-2*X(7) +2*X(20)-4*X(2)-2*X(22)+13*K-2*X(24)-2*X(8)-2*X(26)-2*X(27) -2*X(29)+2*X(30)+4*X(40)) /2 
X(37) = - X(6)- X(34)+ X(35)- X(36)+ X(10)- X(16)+ X(12)- X(18)- X(7)+ X(20)+ X(3)- X(26)+ X(28)- X(29) + X(30)+ X(4)+ X(40) 
X(38) = X(34)+ X(36)- X(10)+ X(18)- X(20)+ K+ X(26)- X(28)- X(30)- X(40) 
X(39) = (-6*X(32)-8*X(6)-4*X(34)+4*X(35)-8*X(36)+12*X(10)+4*X(13)-4*X(16)-4*X(12)-8*X(18) -6*X(7)+6*X(20)+2*X(3)-8*X(2)-6*X(22)+17*K-2*X(24)-4*X(8) -6*X(26)-4*X(27)+4*X(28)-4*X(29)+8*X(30)+10*X(40)) /2 
X(5) = -(4*X(32)+2*X(6)-2*X(34)-2*X(10)+2*X(16)+2*X(12)-2*X(18)+2*X(7)-2*X(20) +2*X(3)+4*X(2)+2*X(22)-9*K+2*X(24)+4*X(8)-2*X(26)-2*X(30) +2*X(4)) /2 
X(9) = -(-2*X(32)+2*X(10)-2*X(12)+2*X(20)-2*X(2)-2*X(22)- K+2*X(30)+2*X(40))/2

В этой формуле мы имеем 24 свободные переменные из 40 при заданной константе ассоциативности K.
Напомню: константа ассоциативности квадрата 9-го порядка связана с его магической константой следующим соотношением: $S=9K/2$.

Проверяю формулу. Задаю константу ассоциативности и произвольные значения свободных элементов квадрата:

K=4226:X(2)=1429:X(3)=919:X(4)=3727:X(7)=3607:X(8)=1039:X(10)=223:X(24)=3583
X(28)=2089:X(30)=1753:X(34)=1669:X(35)=2143:X(36)=1543
X(40)=3877:X(13)=1933:X(6)=2119:X(32)=2545:X(29)=2533:X(27)=3283:X(26)=1471:X(22)=349:X(20)=1861:X(18)=2617:X(12)=1987:X(16)=853

Вычислив по формуле значения зависимых элементов квадрата, получим следующий идеальный квадрат:

4027  1429  919  3727  1441  2119  3607  1039  709 
223  3109  1987  1933  3499  907  853  3889  2617 
1759  1861  3703  349  1459  3583  1549  1471  3283 
2089  2533  1753  1789  2545  2953  1669  2143  1543 
2167  1723  1429  3877  2113  349  2797  2503  2059 
2683  2083  2557  1273  1681  2437  2473  1693  2137 
943  2755  2677  643  2767  3877  523  2365  2467 
1609  337  3373  3319  727  2293  2239  1117  4003 
3517  3187  619  2107  2785  499  3307  2797  199 

$K=4226, S=19017$

Решение в точности совпадает с исходным квадратом, из которого я взяла значения свободных элементов.
Можно считать это решение первым приближением к настоящему решению - идеальному квадрату из различных простых чисел.

Сейчас буду писать программу по общей формуле.
Минимизировать известное решение alexBlack с магической константой 24237, скорее всего, можно. Нижняя граница для магической константы таких квадратов равна 11493.

[Nataly-Mak]

Нахожу массив комплементарных пар простых чисел с константой комплементарности 2554:

3  5  11  23  107  113  131  137  173  197  257  281  311  317  347  401  443  467  491  557  641  647  653  677  683  743  821  857  887  941  947  953  971  983  1031  1061  1103  1181  1187  1193  1361  1367  1373  1451  1493  1523  1571  1583  1601  1607  1613  1667  1697  1733  1811  1871  1877  1901  1907  1913  1997  2063  2087  2111  2153  2207  2237  2243  2273  2297  2357  2381  2417  2423  2441  2447  2531  2543  2549  2551 

Ровно 40 комплементарных пар.
Похоже, что идеальный квадрат 9-го порядка из простых чисел с такой константой ассоциативности построить невозможно.
Программа построения обычного магического квадрата (вероятностный алгоритм) с магической константой $S=9K/2=11493$ буксует.
Не является ли фатальной причиной число 3?

Обычный магический квадрат из следующего потенциального массива с константой ассоциативности 2722 построился по вероятностному алгоритму в долю секунды:

23 509 479 1103 2213 1499 1811 2081 2531
1361 2609 449 1559 1913 2243 1289 173 653
1613 743 2129 2039 1283 1223 1979 1151 89
383 2693 1433 2273 1229 569 1709 389 1571
281 641 683 2069 809 2441 2591 2621 113
911 2663 2549 773 1109 263 1949 29 2003
2333 179 1163 2063 1439 2339 191 2411 131
2711 1619 2543 59 101 1013 11 1493 2699
2633 593 821 311 2153 659 719 1901 2459

$K=2722, S=12249$

Но из всего массива, состоящего из 82 комплементарных пар, сразу выбросила комплементарную пару (3,2719); осталось ровно 40 пар, и квадрат построился мгновенно.
Весь массив:

3  11  23  29  59  89  101  113  131  173  179  191  263  281  311  383  389  449  479  509  569  593  641  653  659  683  719  743  773  809  821  911  1013  1103  1109  1151  1163  1223  1229  1283  1289  1433  1439  1493  1499  1559  1571  1613  1619  1709  1811  1901  1913  1949  1979  2003  2039  2063  2069  2081  2129  2153  2213  2243  2273  2333  2339  2411  2441  2459  2531  2543  2549  2591  2609  2621  2633  2663  2693  2699  2711  2719 

Теперь меня заинтересовал вопрос: а как построить из данного массива ассоциативый магический квадрат 9-го порядка?

Кстати, последовательность A188537 наименьших магических констант ассоциативных квадратов из простых чисел в OEIS обрывается на квадрате порядка 8.
Наименьший ассоциативный квадрат 9-го порядка из (различных) простых чисел ещё не найден.
Наверное, его ещё никто и не искал

[Nataly-Mak]

Цитата:

Но из всего массива, состоящего из 82 комплементарных пар...

Здесь опечатка, правильно так:

Но из всего массива, состоящего из 41 комплементарной пары...
(просто в голове висело количество всех чисел в массиве )

[Nataly-Mak]

Программу для поиска идеального квадрата 9-го порядка по общей формуле написала.
Пока только несколько приближений с 4 дырками, лучше никак – хоть застрелись

Это одно из решений с 4 дырками:

2767 1429 919 3727 883 757 3607 1039 3889
223 3499 1609 1567 3877 2647 853 2239 2503
3457 283 3769 2467 307 3583* 451* 1471 3229
3217 1117 1753 1933 1789 3853 1669 2143 1543
3613 2677 643 3259 2113 967 3583 1549 613
2683 2083 2557 373 2437 2293 2473 3109 1009
997 2755 3775* 643* 3919 1759 457 3943 769
1723 1987 3373 1579 349 2659 2617 727 4003
337 3187 619 3469 3343 499 3307 2797 1459

$K=4226, S=19017$

Неправильные элементы помечены звёздочкой. В решении две неправильные комплементарные пары, при этом одна из комплементарных пар - (643, 3583) из нужных простых чисел состоит, но она повторена!

[Nataly-Mak]

Nataly-Mak в сообщении #985875 писал(а):

Наименьший ассоциативный квадрат 9-го порядка из (различных) простых чисел ещё не найден.
Наверное, его ещё никто и не искал

Теперь найден:

1283 311 1811 2213 1571 569 2039 1163 1289
773 653 2243 1619 2063 593 2693 383 1229
1979 1499 2699 641 821 89 809 2003 1709
1613 2531 101 131 2333 2441 2663 263 173
113 179 2711 449 1361 2273 11 2543 2609
2549 2459 59 281 389 2591 2621 191 1109
1013 719 1913 2633 1901 2081 23 1223 743
1493 2339 29 2129 659 1103 479 2069 1949
1433 1559 683 2153 1151 509 911 2411 1439

$K=2722, S=12249$

-- Вс мар 08, 2015 12:43:42 --

Nataly-Mak в сообщении #982768 писал(а):

Приведу нижние границы для магических констант идеальных квадратов из различных простых чисел, которые уже прикинула (возможны ошибки, просьба к коллегам проверить):

$n=9, S=11493$ центральный элемент 1277;
(известно решение alexBlack с магической константой 24237; минимальность решения не доказана); см. статью;

$n=11, S=24673$ центральный элемент 2243;

$n=13,S=49361$ центральный элемент 3797;

$n=15, S=74595$ центральный элемент 4973.

Для чётных порядков больше 8 пока не вычислила нижние границы, надо искать массивы комплементарных пар.

Для $n=9$ уточняю нижнюю границу: $S=12249$; найден наименьший ассоциативный квадрат с такой магической константой.

Далее привожу нижние границы для магических констант идеальных квадратов чётных порядков:

$n=10, S=4200$;

$n=12,S=8820$;

$n=14, S=16170$;

$n=16, S=21840$.

Первая прикидка. Надеюсь, что не ошиблась.

[Nataly-Mak]

Nataly-Mak в сообщении #987333 писал(а):

Приведу нижние границы для магических констант идеальных квадратов из различных простых чисел...

$n=11, S=24673$ центральный элемент 2243;

Уточняю нижнюю границу для магической константы идеального квадрата 11-го порядка - $S=26521$.
Только что найден минимальный ассоциативный квадрат данного порядка из различных простых чисел.

[svb]

Нижние границы магической константы идеальных квадратов, в которых не используется 3:

(Оффтоп)

$n=7, S=4487$
$n=8, S=2040$
$n=9, S=12249$
$n=10, S=4200$
$n=11, S=26521$
$n=12, S=8820$
$n=13, S=49439$
$n=14, S=16170$
$n=15, S=74595$
$n=16, S=21840$

Почти все совпадает с данными, приведенными Nataly-Mak

[Nataly-Mak]

Вроде не совпадает только для $n=13$.
Не работала ещё над этим ассоциативным квадратом.
Первая прикидка - массив, дающий магическую константу 49361. Но этот потенциальный массив состоит ровно из 84 комплементарных пар и содержит простое число 3 (сейчас его сгенерировала и посмотрела). Поэтому он отпадает.
А следующий потенциальный массив даёт магическую константу 49439. Он тоже содержит простое число 3, но в нём 85 комплементарных пар. Поэтому, выбросив комплементарную пару, содержащую число 3, мы получим массив из 84 пар. Вполне годится.

svb
спасибо за проверку.
Завтра займусь поиском наименьшего ассоциативного квадрата 13-го порядка из различных простых чисел.

[Nataly-Mak]

Покажу три пандиагональных квадрата 16-го порядка из различных простых чисел, иллюстрирующих три метода построения.

№1

19 67 83 109 5953 5927 5903 5879 3203 3049 3229 3547 2837 2969 2797 2477
137 139 157 179 5857 5843 5839 5813 3359 3187 3467 4423 2659 2843 2549 1597
199 223 227 317 5743 5737 5749 5623 3917 3299 3907 4139 2153 2753 2129 1933
347 433 523 607 5563 5347 5443 5209 3863 4229 3413 3803 2239 2003 2633 2393
4253 3319 3739 4007 1787 2699 2287 2017 1069 337 593 569 4903 5657 5393 5419
3709 4507 4349 4597 2309 1523 1667 1423 487 1459 1039 353 5507 4523 4957 5639
4337 3389 4129 4789 1733 2663 1907 1283 619 313 449 967 5323 5647 5527 4973
4019 4793 3623 4283 2083 1439 2423 1913 503 997 733 1087 5407 4783 5233 4729
2803 2957 2777 2459 3169 3037 3209 3529 5987 5939 5923 5897 53 79 103 127
2647 2819 2539 1583 3347 3163 3457 4409 5869 5867 5849 5827 149 163 167 193
2089 2707 2099 1867 3853 3253 3877 4073 5807 5783 5779 5689 263 269 257 383
2143 1777 2593 2203 3767 4003 3373 3613 5659 5573 5483 5399 443 659 563 797
4937 5669 5413 5437 1103 349 613 587 1753 2687 2267 1999 4219 3307 3719 3989
5519 4547 4967 5653 499 1483 1049 367 2297 1499 1657 1409 3697 4483 4339 4583
5387 5693 5557 5039 683 359 479 1033 1669 2617 1877 1217 4273 3343 4099 4723
5503 5009 5273 4919 599 1223 773 1277 1987 1213 2383 1723 3923 4567 3583 4093

$S=48048$

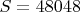
Этот квадрат построен с помощью решёток Россера из 16 пандиагональных квадратов 4-го порядка.
(см. http://www.natalimak1.narod.ru/kompl556.htm )

№2

1087 619 2089 607 1249 677 397 2659 1201 2797 3001 2053 151 1543 2213 2857
1481 1063 421 2801 271 2843 773 1549 857 1697 2767 2731 2593 1013 313 2027
179 1997 3121 2099 683 3019 1483 2221 443 1163 2749 1571 2741 223 601 907
2953 3089 2551 863 2557 1597 181 1367 2777 461 113 1723 1823 109 1409 1627
2267 1777 1933 1493 1721 101 2477 479 2683 2609 839 1019 233 2081 2719 769
193 3119 127 1913 2297 1873 751 139 2939 2503 1871 1831 3083 881 971 709
2711 1283 1289 1583 2803 947 997 1151 691 2791 89 811 2887 3137 241 1789
761 2693 2239 463 2663 1009 2579 2423 41 1619 2341 83 733 3079 1171 1303
1949 353 149 1097 2999 1607 937 293 2063 2531 1061 2543 1901 2473 2753 491
2293 1453 383 419 557 2137 2837 1123 1669 2087 2729 349 2879 307 2377 1601
2707 1987 401 1579 409 2927 2549 2243 2971 1153 29 1051 2467 131 1667 929
373 2689 3037 1427 1327 3041 1741 1523 197 61 599 2287 593 1553 2969 1783
467 541 2311 2131 2917 1069 431 2381 883 1373 1217 1657 1429 3049 673 2671
211 647 1279 1319 67 2269 2179 2441 2957 31 3023 1237 853 1277 2399 3011
2459 359 3061 2339 263 13 2909 1361 439 1867 1861 1567 347 2203 2153 1999
3109 1531 809 3067 2417 71 1979 1847 2389 457 911 2687 487 2141 571 727

$S=25200$

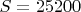
Этот квадрат получен с помощью преобразования 3-х квадрантов из ассоциативного квадрата, построенного методом точных ортогональных покрытий.
(см. post989356.html#p989356 )

№3 (автор Jarek)

(7,109,467,829,1423,349,1607,1129,197,701,1483,401,827,1997,613,1301), (127,809,1567,419,547,509,37,1409,1823,2011,503,31,743,691,1277,937), (1847,1031,1453,1361,1487,641,523,491,1153,1039,137,1699,73,79,47,379), (53,1531,263,211,773,1741,1103,241,277,569,1297,89,1867,1049,1087,1289), (643,1579,677,1609,283,1459,1097,859,617,11,1033,881,1637,191,733,131), (1747,1229,577,479,1237,359,877,719,563,601,293,1231,1193,151,233,1951), (1217,101,163,41,317,761,433,281,1123,769,947,2029,1543,1249,977,1489), (683,811,983,541,1493,661,863,1381,157,1499,607,1319,1447,269,487,239), (1663,739,857,1669,853,139,1307,499,647,1511,43,431,887,911,463,821), (97,179,1657,2069,457,839,997,449,1523,991,383,751,23,1171,1583,271), (17,311,1093,521,1427,1871,1303,1601,1723,1069,557,19,373,619,227,709), (443,331,173,1801,113,61,1223,1051,967,29,2287,1619,787,389,727,1439), (883,1759,797,229,823,439,257,919,587,71,223,251,1367,1571,1783,1481), (2557,1259,907,1019,367,929,337,149,83,421,953,1021,353,1291,1163,631), (347,1091,1213,461,107,1061,193,941,673,1549,2297,1009,13,199,1973,313), (1109,571,593,181,1733,1621,1283,1321,1327,599,397,659,307,1613,67,59)

$S=13440$

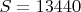
(см. http://trdb.org/Contest/PandiagonalMagi ... inalReport )

Совершенствуются алгоритмы – улучшаются результаты.
И это, скорее всего, ещё не минимальное решение. Согласно последовательности OEIS A164843 нижняя граница магической константы пандиагонального квадрата 16-го порядка из различных простых чисел равна 12088.

[Nataly-Mak]

В той же статье нашла пандиагональный квадрат 12-го порядка из различных простых чисел, построенный по решёткам Россера (из четырёх пандиагональных квадратов 6-го порядка), с магической константой 8820.
Интересно, что этот пандиагональный квадрат превращается в ассоциативный квадрат с помощью преобразования 3-х квадрантов (так как он составлен их комплементарных пар чисел).
Так вот, можно было мне и не строить сейчас методом точных ортогональных покрытий наименьший ассоциативный квадрат 12-го порядка, давно уже построила его. Ну, испытать новый метод не помешало и для порядка 12.

У Jarek результат лучше, у него пандиагональный квадрат данного порядка имеет магическую константу 5544.

Замечание: если ассоциативный квадрат мы превращаем в пандиагональный преобразованием 3-х квадрантов, то обратное превращение пандиагонального квадрата в ассоциативный, понятно, выполняется с помощью обратного преобразования. Но! Преобразование 3-х квадрантов совпадает с обратным ему преобразованием. В статье написано об обратном преобразовании, превращающем пандиагональный квадрат в ассоциативный.
Ну, и ещё замечу, что в последнее время я стала называть данное преобразование "преобразованием 3-х квадрантов" (а не 3-х квадратов).

[Nataly-Mak]

Попытка применить к построению идеального квадрата 9-го порядка метод точных ортогональных покрытий.

Возьмём следующий массив, состоящий из 52 комплементарных пар простых чисел с константой комплементарности 4226:

7  67  73  97  127  199  223  283  307  337  349  373  379  433  457  487  499  613  619  643  709  727  
757  769  853  883  907  919  967  997  1009  1039  1063  1117  1423  1429  1459  1543  1549  1567  1579  
1609  1669  1723  1753  1759  1789  1879  1933  1987  2083  2089  2137  2143  2239  2293  2347  2437  2467  
2473  2503  2557  2617  2647  2659  2677  2683  2767  2797  2803  3109  3163  3187  3217  3229  3259  3307  
3319  3343  3373  3457  3469  3499  3517  3583  3607  3613  3727  3739  3769  3793  3847  3853  3877  3889  
3919  3943  4003  4027  4099  4129  4153  4159  4219 

Это ассоциативный квадрат, построенный из пары точных ортогональных покрытий массива (метод подробно описан в теме «Магические квадраты» ):

3319 2767 1723 3613 7 379 4027 73 3109
1543 97 2647 3877 967 3343 307 3889 2347
4159 2803 619 1063 2239 3217 1039 1789 2089
1933 2083 1429 769 433 3499 1549 3469 3853
2557 3583 2617 3229 2113 997 1609 643 1669
373 757 2677 727 3793 3457 2797 2143 2293
2137 2437 3187 1009 1987 3163 3607 1423 67
1879 337 3919 883 3259 349 1579 4129 2683
1117 4153 199 3847 4219 613 2503 1459 907

$K=4226, S=19017$

Имеем:
первое точное покрытие массива (цепочки-строки):

3319 2767 1723 3613 7 379 4027 73 3109
1543 97 2647 3877 967 3343 307 3889 2347
4159 2803 619 1063 2239 3217 1039 1789 2089
1933 2083 1429 769 433 3499 1549 3469 3853
2557 3583 2617 3229 2113 997 1609 643 1669
373 757 2677 727 3793 3457 2797 2143 2293
2137 2437 3187 1009 1987 3163 3607 1423 67
1879 337 3919 883 3259 349 1579 4129 2683
1117 4153 199 3847 4219 613 2503 1459 907

Второе точное покрытие массива (цепочки-столбцы), ортогонально первому покрытию:

3319 1543 4159 1933 2557 373 2137 1879 1117
2767 97 2803 2083 3583 757 2437 337 4153
1723 2647 619 1429 2617 2677 3187 3919 199
3613 3877 1063 769 3229 727 1009 883 3847
7 967 2239 433 2113 3793 1987 3259 4219
379 3343 3217 3499 997 3457 3163 349 613
4027 307 1039 1549 1609 2797 3607 1579 2503
73 3889 1789 3469 643 2143 1423 4129 1459
3109 2347 2089 3853 1669 2293 67 2683 907

Здесь всё чётко.
Теперь надо найти ещё два точных покрытия массива ортогональные друг другу и первым двум точным покрытиям. Одно покрытие будет цепочки-диагонали прямые, другое – цепочки-диагонали обратные.
Можно уже сразу написать по одной цепочке в искомых точных покрытиях массива.

Прямая диагональ (главная):

3319 97 619 769 2113 3457 3607 4129 907

Обратная диагональ (главная):

3109 3889 1039 3499 2113 727 3187 337 1117

Решаема ли поставленная задача

Коллеги, ау! У меня уже мозги всмятку Кто-нибудь поможет?

[Nataly-Mak]

Есть первый идеальный квадрат 10-го порядка из различных простых чисел
Долго же я его искала поиск был начат в 2008 г., как только alexBlack нашёл первые идеальные квадраты 7-го и 9-го порядков из простых чисел (идеалный квадрат 8-го порядка был найден мной).
Наконец-то поиск увенчался успехом.

Сейчас пытаюсь таким же методом найти идеальный квадрат 11-го порядка из различных простых чисел. Пока нет даже хорошего приближения к решению. Трудновато. Общая формула идеального квадрата 11-го порядка содержит 40 свободных переменных из 60 при заданной константе ассоциативности.
Вот эта формула:

(Оффтоп)

X(1) = -(-4*X(52)-2*X(55)+3*K-4*X(16)-2*X(8)-4*X(57)-4*X(22)+2*X(23)+4*X(15) +2*X(3)-2*X(26)-4*X(27)-2*X(28)+4*X(29)-2*X(30)+4*X(10)-2*X(58) -4*X(32)-6*X(33)+4*X(34)+2*X(35)-4*X(36)+6*X(4)-2*X(38)+2*X(39) +2*X(40)+6*X(9)+4*X(59)-2*X(43)-4*X(44)+2*X(45)-4*X(46)-4*X(47) +6*X(5)+2*X(7)) /4 
     
X(11) = -(4*X(53)+4*X(54)+6*X(55)-21*K-4*X(16)-2*X(8)-4*X(57)+4*X(22)+6*X(23) -4*X(15)-2*X(3)-2*X(26)-12*X(27)-2*X(28)+4*X(29)-2*X(30)+12*X(10) -2*X(58)-4*X(32)-2*X(33)+6*X(35)+6*X(4)-6*X(38)-6*X(39)+6*X(40) +2*X(9)+8*X(59)-
4*X(42)+2*X(43)+2*X(45)+8*X(47)+4*X(48)+2*X(5) +4*X(50)+6*X(7)) /4   

X(12) = (-4*X(52)+3*K-4*X(16)-2*X(8)-2*X(57)-2*X(22)+2*X(23)-4*X(27)-2*X(28) +4*X(29)+4*X(10)-4*X(32)-2*X(33)+2*X(34)+2*X(35)-2*X(36)+2*X(4) -2*X(38)+2*X(40)+4*X(9)+4*X(59)-2*X(42)-2*X(43)-2*X(44)+2*X(5) +2*X(50)+2*X(7)) /2 
  
X(13) = (-2*X(52)-2*X(53)-4*X(54)-2*X(55)+11*K+2*X(16)+2*X(8)-4*X(22)-6*X(23) +4*X(15)+2*X(3)+6*X(27)+2*X(28)-2*X(29)-4*X(10)+2*X(58)-4*X(35) +4*X(38)+4*X(39)-2*X(40)-4*X(59)-2*X(44)-2*X(45)-2*X(46)-6*X(47) +2*X(5)-2*X(50)-2*X(7)+2*X(60)) /2 
  
X(14) = (-2*X(55)+3*K-4*X(16)+2*X(8)+4*X(57)+2*X(23)-4*X(15)-2*X(3)-2*X(26) -2*X(28)+2*X(30)+2*X(58)+2*X(33)+2*X(35)-6*X(4)-2*X(38)-2*X(39) -2*X(40)+2*X(9)-2*X(43)+2*X(45)+4*X(46)+4*X(47)-2*X(5)+2*X(7)) /4
   
X(17) = 2*X(52)+ X(54)+ X(55)-5*K+ X(8)+ X(57)+2*X(22)+ X(23)-2*X(15)- X(3)- X(27)- X(29) +2*X(32)+ X(33)+ X(35)+ X(36)- X(4)- X(39)- X(9)+ X(42)+ X(43)+2*X(44)+ X(45) + X(46)+2*X(47)-2*X(5)- X(60) 
  
X(18) = - X(52)- X(53)- X(54)- X(55)+6*K+ X(16)-2*X(22)-2*X(23)+2*X(15)+2*X(3)+3*X(27) - X(29)-2*X(10)-2*X(35)+ X(38)+2*X(39)- X(40)-2*X(59)- X(45)- X(46)-3*X(47) - X(48)+ X(5)- X(50)- X(7)+ X(60)
   
X(19) = (-2*X(52)+4*X(53)+4*X(54)+2*X(55)-7*K-4*X(16)-4*X(8)-4*X(57)+6*X(23)-2*X(15) -2*X(3)-8*X(27)-2*X(28)+4*X(29)+8*X(10)-2*X(58)-4*X(32)-2*X(33) +2*X(34)+4*X(35)-2*X(36)+4*X(4)-4*X(38)-4*X(39)+4*X(40)+2*X(9) +6*X(59)-2*X(42)-2*X(44)+2*X(45)+4*X(47)+2*X(48)+2*X(5)+4*X(50) +2*X(7)) /2  
 
X(2) = (2*X(54)+ K-2*X(8)-2*X(57)+2*X(23)-2*X(27)+2*X(29)+2*X(10)-2*X(58)-2*X(33) +2*X(4)-2*X(38)+2*X(40)+2*X(59)-2*X(46)) /2 
  
X(20) = -(-8*X(52)-2*X(55)+ K-4*X(16)-2*X(8)-4*X(57)-8*X(22)+2*X(23)+4*X(15) +2*X(3)-2*X(26)-4*X(27)-2*X(28)+4*X(29)+2*X(30)+8*X(10)-2*X(58) -8*X(32)-6*X(33)+4*X(34)+2*X(35)-4*X(36)+6*X(4)-2*X(38)+2*X(39) +6*X(40)+6*X(9)+4*X(59)-4*X(42)-2*X(43)-4*X(44)+2*X(45)-4*X(46) -4*X(47)+6*X(5)+4*X(50)+2*X(7)+4*X(60)) /4
   
X(21) = -(-2*X(52)- K-2*X(16)-2*X(28)+2*X(58)+2*X(33)+2*X(34)-2*X(4)-2*X(40) +2*X(9)+2*X(46)) /2 
  
X(24) = 2*X(52)+ X(53)+2*X(54)+ X(55)-5*K+2*X(22)+2*X(23)-2*X(15)- X(3)-2*X(27)+2*X(10) - X(58)+ X(32)- X(34)+ X(35)- X(38)-2*X(39)+ X(40)- X(9)+ X(59)+ X(43)+ X(44)+ X(45) +3*X(47)- X(5)+ X(50)+ X(7)- X(60)  
 
X(25) = - X(54)+5*K+ X(16)-2*X(23)+ X(15)+ X(27)- X(29)- X(30)-2*X(10)- X(35)+ X(38)+ X(39) - X(40)- X(59)+ X(42)- X(45)-2*X(47)- X(50)- X(7)
   
X(31) = (-4*X(52)-2*X(53)-2*X(54)-2*X(55)+11*K-2*X(16)-4*X(22)-2*X(23)+2*X(15) +2*X(3)-2*X(26)-2*X(28)+2*X(58)-4*X(32)-2*X(33)+2*X(34)+2*X(39) +2*X(9)-2*X(42)-2*X(43)-2*X(44)-2*X(47)+2*X(5)+2*X(60)) /2 
  
X(37) = (4*X(53)+4*X(54)+2*X(55)+5*K-4*X(16)-2*X(8)-4*X(57)+6*X(23)-4*X(15)-2*X(3) -2*X(26)-8*X(27)-2*X(28)+4*X(29)+2*X(30)+8*X(10)-2*X(58)-4*X(32) -2*X(33)+2*X(35)-4*X(36)+2*X(4)-6*X(38)-6*X(39)+2*X(40)+2*X(9) +4*X(59)-4*X(42)-2*X(43)-4*X(44)+2*X(45)+4*X(47)+2*X(5)+4*X(50) +2*X(7)) /4 
  
X(41) = -(4*X(53)+4*X(54)+2*X(55)-17*K-4*X(16)-2*X(8)-4*X(57)+6*X(23)-4*X(15) -2*X(3)-2*X(26)-8*X(27)-2*X(28)+4*X(29)+2*X(30)+8*X(10)-2*X(58) -4*X(32)-2*X(33)+4*X(34)+6*X(35)+2*X(4)-2*X(38)-2*X(39)+6*X(40) +2*X(9)+4*X(59)+2*X(43)+2*X(45)+4*X(47)+2*X(5)+4*X(50)+2*X(7)) /4
   
X(49) = - X(52)- X(53)- X(54)- X(55)+6*K- X(22)- X(23)+ X(15)+ X(3)+ X(27)- X(10)- X(35)+ X(39) - X(59)- X(45)- X(46)-2*X(47)- X(48)- X(50)
   
X(51) = (- K+2*X(22)+2*X(23)-2*X(15)-2*X(3)-2*X(27)+2*X(10)+2*X(35)-2*X(39) +2*X(59)+2*X(47)) /2 
  
X(56) = X(52)- X(53)- X(54)- X(55)+5*K+2*X(16)+ X(8)+ X(57)-3*X(23)+2*X(15)+ X(3)+4*X(27) + X(28)-2*X(29)-4*X(10)+2*X(32)+ X(33)- X(34)-2*X(35)- X(4)+2*X(38)+2*X(39) -2*X(40)- X(9)-3*X(59)+2*X(42)+ X(44)- X(45)- X(46)-3*X(47)- X(48)-2*X(50) -2*X(7) 
  
X(6) = (-2*X(52)+2*X(53)+2*X(55)+ K-4*X(16)-2*X(8)-2*X(57)+2*X(23)-2*X(3)-2*X(26) -6*X(27)-2*X(28)+2*X(29)-2*X(30)+4*X(10)-4*X(32)-2*X(33)+2*X(34) +4*X(35)-2*X(36)+2*X(4)-2*X(38)-2*X(39)+2*X(40)+2*X(9)+4*X(59) -2*X(42)-2*X(44)+2*X(45)+2*X(47)+2*X(48)+2*X(5)+2*X(50)+2*X(7)) /2

Формулу проверила и на классическом, и на нетрадиционном идеальных квадратах.
Например, для классического идеального квадрата, вводим значения свободных элементов и константы ассоциативности (понятно, что в этом примере значения свободных элементов взяты из известного классического идеального квадрата; если их задать произвольно, то классический квадрат может и не получиться):

K=122
X(3)=74:X(4)=105:X(5)=15:X(7)=88:X(8)=119:X(9)=29:X(10)=60
X(15)=86:X(16)=117:X(22)=72:X(23)=84:X(26)=56:X(27)=98
X(28)=8:X(29)=39:X(30)=70:X(32)=22:X(33)=53:X(34)=65:X(35)=96:X(36)=6:X(38)=68:X(39)=110:X(40)=20
X(42)=82:X(43)=113:X(44)=23:X(45)=35:X(46)=77:X(47)=108:X(48)=18:X(50)=80:X(52)=32:X(53)=63
X(54)=94:X(55)=4:X(57)=47:X(58)=78:X(59)=120:X(60)=30

Вычислив по формуле значения зависимых элементов, получаем следующий классический идеальный квадрат:

1 43 74 105 15 46 88 119 29 60 91 
103 13 55 86 117 27 58 89 10 41 72 
84 115 25 56 98 8 39 70 101 22 53 
65 96 6 37 68 110 20 51 82 113 23 
35 77 108 18 49 80 111 32 63 94 4 
16 47 78 120 30 61 92 2 44 75 106 
118 28 59 90 11 42 73 104 14 45 87 
99 9 40 71 102 12 54 85 116 26 57 
69 100 21 52 83 114 24 66 97 7 38 
50 81 112 33 64 95 5 36 67 109 19 
31 62 93 3 34 76 107 17 48 79 121

$K=122, S=671$

[Nataly-Mak]

Пока только такое приближение к решению - идеальному квадрату 11-го порядка из различных простых чисел:

443* 5897 89 3041 2357 131 4649 4919 3119 5741 2273*
3167* 0 0 4241 1487 0 0 0 0 227 4787
4217 0 467 1187 4637 587 557 5867 0 5417 281
5477 2087 2729 3701 1217 5237 2687 431 3797 839 4457
641 2999 269 3557 0 3011 0 4679 3329 5009 3407
4229 5801 3347 4877 0 2969 0 1061 2591 137 1709
2531 929 2609 1259 0 2927 0 2381 5669 2939 5297
1481 5099 2141 5507 3251 701 4721 2237 3209 3851 461
5657 521 0 71 5381 5351 1301 4751 5471 0 1721
1151 5711 0 0 0 0 4451 1697 0 0 2771*
3665* 197 2819 1019 1289 5807 3581 2897 5849 41 5495*

$K=5938, S=32659$
Помеченные звёздочкой три комплементарные пары уже неправильные (в программе отпустила эти пары).
В дырках вообще всё плохо: перекос ужасный, то есть имеются отрицательные числа и числа слишком большие (не в диапазоне).
Вопреки ожиданию для порядка 11 всё намного хуже, чем для порядка 10. Что-то нужно кардинально менять в алгоритме.

[Nataly-Mak]

Nataly-Mak в сообщении #994924 писал(а):

Есть первый идеальный квадрат 10-го порядка из различных простых чисел
Долго же я его искала поиск был начат в 2008 г., как только alexBlack нашёл первые идеальные квадраты 7-го и 9-го порядков из простых чисел (идеалный квадрат 8-го порядка был найден мной).

Прошу прощения, ошиблась
Конечно, это было не в 2008, а в 2011 г.
(посмотрела топик со своим конкурсом здесь, и глянула почему-то не в правый верхний угол - на дату создания топика, а на дату своего появления на форуме; такой заскок бывает)