Нормировка корневых векторов

[Bulinator]

Привет всем.

Возникла следующая проблема. Буду благодарен если отошлете к книгам(с указанием автора и названия).

Итак, есть разложение Картана алгебры Ли $\mathfrak{g}$ на корневые пространства $\mathfrak{g}_\alpha$ и пусть скобки $\langle \cdot ,\cdot \rangle$ обозначают Киллингову форму.

Выберем корневые вектора $e_\alpha$ из соответствующих $\mathfrak{g}_\alpha$.

Вопрос: как выразить $\langle e_\alpha ,e_\alpha \rangle$ через $\langle e_\alpha ,e_{-\alpha} \rangle$?

Заранее спасибо.

-- Чт июн 13, 2013 14:28:31 --

Вопрос 2: насколько тупо следующее утверждение?

Т.к. матрица $ad_{e_\alpha}$- суть нильпотентная матрица, все ее собственные значения равны нулю. А значит, равно нулю так же выражение

$$\langle e_\alpha,e_\alpha\rangle=Tr\left(ad_{e_\alpha},ad_{e_\alpha}\right)=0$$

[scwec]

По первому вопросу и вообще по теме, рекомендую С.Хелгасон "Дифференциальная геометрия и симметрические пространства" 1964.
Глава 3. Книга очень богата содержанием, с прозрачным изложением, хоть и не молодая.
По второму вопросу, с чего Вы взяли, что эта матрица нильпотентная?
И надо было хоть написать, что исходная Алебра Ли полупростая над $\mathbb{C}$.

[Bulinator]

scwec в сообщении #736474 писал(а):

По второму вопросу, с чего Вы взяли, что эта матрица нильпотентная?

Потому что $ad_{e_\alpha}e_\beta=[e_\alpha,e_\beta]\sim e_{\alpha+\beta}$, т.е. $e_\alpha$ действует как повышающий/понижающий(в зависимости от знака корня $\alpha$) оператор. Для любой пары $(\alpha,\beta)$ существует $p\in \mathbb{N}$ такое, что $\beta+p \alpha$ уже не корень(по ходу - 4). Т.е.

$$ ad_{e_\alpha}^p e_\beta=0 $$

Далее допустим, что $g\in\mathfrak{g}$ является собственным вектором $ad_{e_\alpha}$ с собственным значением $\lambda$:

$$ ad_{e_\alpha}g=\lambda g $$

Понятно, что существует $p'$ такое, что

$$ ad^{p'}_{e_\alpha}g=\lambda^{p'}g=0. $$

Вывод:

$$ ad^{p'}_{e_\alpha}=0,\quad \lambda=0,\quad \forall \alpha\in \Phi. $$

Или я чего-то не понимаю?

[scwec]

Алгебра Ли $g$ - полупростая. Фома Киллинга на ней невырождена, поэтому $\langle{e_\alpha},e_\alpha\rangle\ne{0}$.
И вывод из вопроса $2$ неверен. Вместе с ним неверна и посылка о нильпотентности $ad_{e_\alpha}$. Согласны?
Оправдание этому содержит ошибку уже в первых 3-х строках Вашего предыдущего сообщения. Да и дальше не очень внятно. Посмотрите ещё раз повнимательней. Хелгасон должен Вам помочь. Если же Вы с ним хорошо знакомы, то тогда не знаю, что и присоветовать.

[Bulinator]

Я тогда вообще ничего не понимаю. Вектора $e_\alpha$ в присоедененном представлении имеют вид верхнетреугольных матриц. Понятно, что след от их произведения равен нулю.

[scwec]

Может быть, Вы что-то имеете в виду, не имеющее отношение к разложению полупростых алгебр на корневые пространства?
Да вроде нет. И обозначения похожи. Исходная алгебра Ли-то у Вас полупростая? Может, Вы придумали работать с произвольными алгебрами Ли?

[Bulinator]

Давайте посчитаем в лоб. Возьмем алгебру $su(2)$:

$$ [t_z,t_\pm]=\pm t_\pm,\quad [t_+,t_-]=2t_z. $$

Тогда, после некоторой рутины в базисе $(t_+,t_z, t_-)$ получим:

$$ ad_{t_+}=\left(\begin{array}{ccc}0&-1&0\\ 0&0&2\\ 0&0&0 \end{array}\right),\quad ad_{t_-}=\left(\begin{array}{ccc}0&0&0\\ -2&0&0\\ 0&1&0 \end{array}\right),\quad ad_{t_z}=\left(\begin{array}{ccc}1&0&0\\ 0&0&0\\ 0&0&-1 \end{array}\right) $$

Легко видеть, что

$$ ad^2_{t_+}=\left(\begin{array}{ccc}0&0&-2\\ 0&0&0\\ 0&0&0 \end{array}\right) $$

а значит:

$$\operatorname{Tr}(ad^2_{t_+})=0.$$

-- Пт июн 14, 2013 18:02:01 --

И, кстати, $ad^3_{t_\pm}=0$.

[scwec]

Проверьте подсчет $ad$. И потом, если выбрать стандартный базис $su(2)$ в пространстве косоэрмитовых 2х2 матриц со следом $0$ - $s_1,s_2,s_3$ и $[s_1,s_2]=2s_3, [s_2,s_3]=2s_1, [s_3,s_1]=2s_2$, то там никаких странностей с нильпотентностью не происходит (она не появляется).
У Вас-то в базисе не очень понятны выражения для коммутаторов $[t_z,t_\pm]=\pm{t_\pm}$(?) Вы, если можно, напишите их раздельно.

[Bulinator]

Обозначим $t_+=\frac12(s_1+ s_2),t_-=\frac12(s_1-s_2), t_z=s_3$. Тогда, легко видеть, что
$[t_+,t_z]= -2t_+$ и.т.д.
Это делается для того, чтобы $t_\pm$ были корневыми векторами подалгебры Картана $t_z$.

-- Сб июн 15, 2013 11:04:41 --

А насчет нильпотентности в стандартном базисе я не понял. Они же не являются присоединенным представлением.

[scwec]

Об отсутствии нльпотентности в стандартном базисе. Имелось в виду, что матрицы операторов $ad_{s_i}$ не являются нильпотентными.
Теперь, когда $t_{-},t_{+},t_z$ определены через $s_i$, можно написать, что $[t_{+},t_z]=-2t_{-},[t_{-},t_z]=-2t_{+}, [t_-,t_+]=t_z$, что Вы и сделали. За базис считаем $(t_-,t_+,t_z)$
Все соответствующие матрицы присоеденённого представления не нильпотентны. Так, в $ad_{t_-}$ двойка переедет во второй строке на третью позицию, на первой позиции ноль. В $ad_{t_+}$ двойка и -1 тоже разъедутся по разные стороны главной диагонали. Проверьте.

[type2b]

in the standard decomposition of a simple Lie algebra $\mathfrak{n}_-\oplus \mathfrak{h}\oplus \mathfrak{n}_+$ the subalgebras $\mathfrak{n}_\pm$ are, of course, nilpotent, so the corresponding matrices in the adjoint representation are nilpotent. As TS correctly says, a Killing norm of a nilpotent generator is zero.

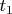
Here there is no contradiction with the non-degeneracy of the Killing form, because this is a bilinear form on the complex algebra, not a hermitian form. E.g., if $t_1$ and $t_2$ are orthonormal vectors in a real vector space, then $(t_1+it_2,t_1+it_2)=(t_1,t_1)-(t_2,t_2)=0$.

One should NOT say that $t_\pm$ belong to the real algebra $\mathfrak{su}(2)$. They live in the complex algebra $\mathfrak{sl}_\mathbb{C}(2)$.

[Bulinator]

type2b в сообщении #737186 писал(а):

They live in the complex algebra $\mathfrak{sl}_\mathhb{C}(2)$.

And for any semisimple Lie algebra the root vectors shoud live not in algebra itself but in the universal enveloping one. Is it true?

[type2b]

[Bulinator]

Сорри, ляпнул. Правильно будет так, что корневые вектора вещественной алгебры Ли живут в ее комплексифицированной. Да?

[type2b]

вы хотели сказать, что корневые вектора не принадлежат никакой вещественной форме? Это не так, см. $sl_{\mathbb{R}}(2)$.
Для простой алгебры они не принадлежат компактной вещественной форме.