Системы множеств

[djuuj]

Вот такие вопросы.
1. Собственно, теорема о порожденной $\sigma$-алгебре из "Элементов" Колмогорова, Фомина (издание 6, гл.1, §5, п.4, теорема 4):
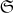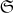Для любой непустой системы множеств $\mathfrak S$ существует неприводимая (по отношению к этой системе) $\sigma$-алгебра $\mathfrak B(\mathfrak S)$, содержащая $\mathfrak S$ и содержащаяся в любой $\sigma$-алгебре, содержащей $\mathfrak S$.
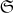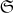
Под неприводимой по отношению к $\mathfrak S$ $\sigma$-алгеброй понимается "$\sigma$-алгебра, не содержащая точек, не входящих ни в одно из $A \in \mathfrak S$" (таким образом, её единица совпадает с $\bigcup \limits_{A \in \mathfrak S} A$). Вместо доказательства автор пишет, что оно "проводится в точности тем же методом", что и аналогичная теорема о порожденном кольце.
Доказать теорему в такой формулировке у меня не получается (пересечение произвольных $\sigma$-алгебр вроде бы не обязательно $\sigma$-алгебра). Мне кажется теорема сформулирована не совсем точно. Видимо имелось в виду, что $\mathfrak B(\mathfrak S)$ содержится в любой в любой неприводимой (а не вообще любой) $\sigma$-алгебре, содержащей $\mathfrak S$.
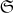
Если я прав, хотелось бы посмотреть на пример, опровергающий теорему без этого уточнения. Если нет, то доказательство.
И ещё. Кажется, что в теореме можно добавить, что такая $\sigma$-алгебра единственна, и теорема останется справедливой. Странно, что в учебнике это не написано..

2. В том же учебнике в гл.1, §5, п.5 читателю предлагается проверить справедливость следующих утверждений. Пусть $f$ -- отображение из $M$ в $N$, $\mathfrak N$ -- некоторая непустая система множеств, содержащихся в $N$, и $f^{-1}(\mathfrak N)$ -- система всех прообразов $f^{-1}(A)$ множеств, входящих в $\mathfrak N$. Тогда

$$ \mathfrak R(f^{-1}(\mathfrak N)) = f^{-1}(\mathfrak R(\mathfrak N)), $$

$$ \mathfrak B(f^{-1}(\mathfrak N)) = f^{-1}(\mathfrak B(\mathfrak N)). $$

Здесь $\mathfrak R(\mathfrak N)$ -- кольцо, порожденное $\mathfrak N$, $\mathfrak B(\mathfrak N)$ -- $\sigma$-алгебра, порожденная $\mathfrak N$. Просьба помочь с доказательством.

[djuuj]

2. Доказал наконец-то... Выкладываю доказательство, может кому-то будет интересно.
В основе док-ва лежат соотношения: для любой системы $\mathfrak N$ подмножеств $N$ и любых $B_1,B_2 \subseteq N$
\begin{align*} &f^{-1}\left( \bigcup \limits_{B \in \mathfrak N} B\right) = \bigcup \limits_{B \in \mathfrak N} f^{-1}(B),\\ &f^{-1}(B_1 \triangle B_2) = f^{-1}(B_1) \triangle f^{-1}(B_2). \end{align*}
Их можно найти в том же КФ (гл.1, §2).

Итак, пусть $Y=\bigcup \limits_{B \in \mathfrak N} B$ -- единица $\sigma$-алгебры $\mathfrak B(\mathfrak N)$, $X=\bigcup \limits_{B \in \mathfrak N} f^{-1}(B) = f^{-1}\left(\bigcup \limits_{B \in \mathfrak N} B\right) = f^{-1}(Y)$ -- единица $\mathfrak B(f^{-1}(\mathfrak N))$.
$\mathfrak N \subseteq \mathfrak B(\mathfrak N) \Rightarrow f^{-1}(\mathfrak N) \subseteq f^{-1}(\mathfrak B(\mathfrak N))$. Т.к. $f^{-1}(\mathfrak B(\mathfrak N))$ есть $\sigma$-алгебра с единицей $X$ (легко проверяется, используя соотношения), то отсюда следует, что $\mathfrak B(f^{-1}(\mathfrak N)) \subseteq f^{-1}(\mathfrak B(\mathfrak N))$.

Пусть теперь $S=\{ B \subseteq Y:\ f^{-1}(B) \in \mathfrak B(f^{-1} (\mathfrak N)) \}$. Тогда, если $B_1, B_2, \ldots \in S$, то
\begin{align*} &f^{-1}\left(\bigcup \limits_{n=1}^{\infty} B_n \right) = \bigcup \limits_{n=1}^{\infty} f^{-1}(B_n) \in \mathfrak B(f^{-1} (\mathfrak N)),\\ &f^{-1}(B_1 \triangle B_2) = f^{-1}(B_1) \triangle f^{-1}(B_2) \in \mathfrak B(f^{-1} (\mathfrak N)),\\ &f^{-1}(Y)=X \in \mathfrak B(f^{-1}(\mathfrak N)). \end{align*}
Отсюда ясно, что $S$ -- $\sigma$-алгебра с единицей Y. Поэтому, т.к. $\mathfrak N \subseteq S$ (по определению $S$), то $\mathfrak B(\mathfrak N) \subseteq S \Rightarrow f^{-1}(\mathfrak B(\mathfrak N)) \subseteq f^{-1}(S) \subseteq \mathfrak B(f^{-1}(\mathfrak N))$ (последнее включение по определению $S$). Объединяя два включения, получаем $\mathfrak B(f^{-1}(\mathfrak N)) = f^{-1}(\mathfrak B(\mathfrak N))$.

Для колец утверждение доказывается аналогично (даже проще).