Здравствуйте! Пытаюсь вычислить следующую сумму:

где
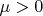
,

,

,

и

,
где

,

, и

, и

находится из условия

.
Я реализовал расчет этой величины в МАТЛАБ, она работает, но имеет нестабильность при маленьких

, порядка 0.01 или меньше, и когда

или больше.
Дело в том, что ряд под суммой - знакопеременный, и состоит из больших по амплитуде членов. Проконсультируйте, пожалуйста, как можно просуммировать этот ряд более устойчивым методом? Я пытался отдельно сложить положительные и отрицательные члены - не работает.
Смысл этих величин - это вероятности определенных событий, т.е. ответ должен быть всегда между 0 и 1.
Спасибо заранее.