Доказать изоморфизм.

[noooob]

Задача:

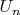
Для каждого натурального $n$ обозначим через $U_n$ подгруппу в $GL_n(R)$ , состоящую из верхнетреугольных матриц с единицами на главной диагонали. Пусть $H$ - подгруппа в $U_4$ , состоящая из тех матриц,у которых все элементы, кроме элементов первой строки и главной диагонали, равны нулю. Докажите, что $U_4 / H \cong U_3$

Решение:

Нужно использовать теорему о гоморфизме групп? Вот эту:

$C_1, C_2$ - группы
$\varphi \in Hom(C_1, C_2)$
Тогда: $ \operatorname{Im} \varphi \cong C_1 / \operatorname{Ker}\varphi $


Смотрю, как решали на практике в универе.
1 пункт - придумать гомоморфизм. У меня, я так понимаю он задан:
$ \varphi : \left( \begin{array}{cccc} 1 & n_1 & n_2 & n_3 \\ 0 & 1 & a & b \\ 0 & 0 & 1 & c \\ 0&0&0&1 \end{array} \right)$ $\mapsto$ $\left( \begin{array}{ccc} 1 & a & b \\ 0 & 1 & c \\ 0&0&1 \end{array} \right)$

2 пункт - применить теорему о гомоморфизмах.

Честно, совсем не понимаю, что тут происходит. Посоветуйте может что почитать ? Ссылочку лучше, учебники искать уже некогда..

[sopor]

Проверьте, что будет ядром вашего гомоморфизма, т.е какие матрицы перейдут в единичную.

[noooob]

Ядро гомоморфизма общих групп - прообраз единицы.
Ну значит вот такие матрицы:
$ \left( \begin{array}{cccc} 1 & n_1 & n_2 & n_3 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0&0&0&1 \end{array} \right)$
перейдут в единичные.

[a_nn]

ну вот и доказали.