Исследовать на абсолютную и условную сходимость ряд

заменой на эквивалентные пришел к сумме

пытаюсь применить к последним слагаемым признак Дирихле, но не могу понять как доказать ограниченность частичных сумм.
Рассматривается при
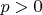
иначе очевидно расходится