1) Пусть X --- внутренняя точка

, B --- окрестность X, целиком состоящая из точек

. Воспользуйтесь тем, что

плотно в B, а затем воспользуйтесь выпуклостью S. Для произвольного S это свойство может и не выполняться (пример очень легко придумать).
2) Во-первых,

. Пусть

, тогда
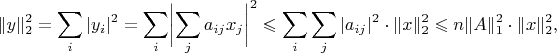
значит,

. Осталось придумать матрицу, для которой выполняется равенство. Это несложно сделать, проанализировав док-во.
3) Это весьма нетривиальный факт, док-во которого можно найти, например, в книге Колмогоров А.Н., Фомин С.В. "Элементы теории функций и функционального анализа" в дополнении про банаховы алгебры (в четвёртом издании 1976 г. это точно есть). Думаю, что док-во можно найти во многих других книжках по функциональному анализу.
Upd.1 Хотя для матриц это, наверное, можно доказать как-нибудь попроще из тех соображений, что этот предел не зависит от нормы (поскольку все нормы эквивалентны), поэтому осталось придумать норму, для которой это легко доказать.
Upd.2 Это легко доказать, например, для нормы

с помощью жордановой нормальной формы. Делается это так. Легко показать, что для любой матрицы выполнено

(это верно для любой матричной нормы), следовательно,
![$\rho(A)\leqslant\varliminf\limits_{k\to\infty}\sqrt[k]{\|A^k\|_1}$ $\rho(A)\leqslant\varliminf\limits_{k\to\infty}\sqrt[k]{\|A^k\|_1}$](https://dxdy-02.korotkov.co.uk/f/9/6/e/96e3384853f582778c5fb35d4fcc4b3882.png)
. Переходя к ЖНФ, несложно получить, что
![$\varlimsup\limits_{k\to\infty}\sqrt[k]{\|A^k\|_1}\leqslant\rho(A)$ $\varlimsup\limits_{k\to\infty}\sqrt[k]{\|A^k\|_1}\leqslant\rho(A)$](https://dxdy-02.korotkov.co.uk/f/d/a/a/daa8989ac472b7a44215c474a00819d582.png)
.