GlazkovD писал(а):
Bot. Может быть я чего то не понял в вашем ответе, но на мой взгляд выражение справедливо не только для

Если имеем тождество

, то какой должна быть функция
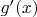
?
В Вашем примере

:

Более коротко это пишется (и называется как сказал
Brukvalub) методом подведения под знак дифференциала:

[отщипываем множитель 3, чтобы занести его под дифференциал]

[так как

, подводим 3 под дифференциал]

[так как

]
Замену

, а потом обратно

здесь делать нет никакой необходимости.