Предположим, что

"имеет степень"

, тогда

"имеет степень"

, а

- "степень"

;

имеет степень

. Приравнивая "степени" членов, получим

; все равенства выполняются при

, поэтому это обобщённо однородное уравнение.
Делаем замену переменной

, где

- новая неизвестная функция. Из условия существования корня получаем
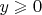
; так как

, то и

. Тогда

, и уравнение принимает вид

где нужно взять знак "

" при

и знак "

" при

. После упрощений получаем

то есть, уравнение с разделяющимися переменными.
Чтобы не запутаться с этими "плюс-минусами", лучше решить уравнение отдельно для

и для

.
Не забудьте, что при разделении переменных могут теряться решения, если то, на что Вы делите, может обращаться в

.