Немного помучившись, я решил, что имеет смысл рассказать здесь, на форуме, что я пытаюсь сделать, полностью. Авось кто-нибудь что-нибудь посоветует. Правда, я не уверен, что раздел подходящий, т. к. это не совсем учебная задача (в том смысле что она не взята из какого-то учебника).
Итак, моя задача - решить задачу о туннелировании (рассчитать прозрачность барьера), используя формализм, обычно применяющийся в КТП. Отправная точка - одноэлектронный гамильтониан

.
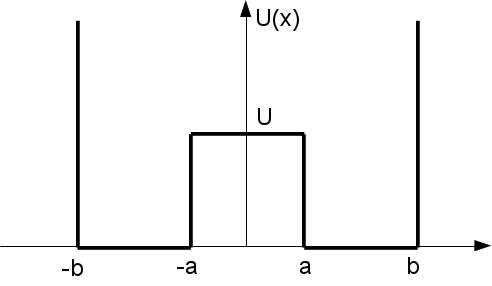
Итак, вот что я делаю. Вначале я разделяю область на три несвязанных прямоугольных ямы с бесконечно высокими стенками и для каждой ямы нахожу стационарные электронные состояния

. Таким образом, я получаю ортонормированный набор одноэлектронных волновых функций, который я использую для построения пространства Фока. И тут я сталкиваюсь с первой трудностью (на ней я пока и засел) - набор неполный! Пока я рассматриваю три раздельных ямы это нормально, но следующим этапом по моему плану идёт "объединение" ям (возвращение к исходной задаче). При этом мне надо, используя имеющееся пространство Фока, построить многоэлектронный гамильтониан

(действующий в этом пространстве) из одноэлектронного

. Очевидно, вначале для этого надо найти матричные элементы одноэлектронного гамильтониана

.
И вот тут в одном месте я упираюсь в несколько взаимосвязанных проблем: 1) набор одноэлектронных функций неполный, т. к. нет ни одной функции, необращающейся в ноль при

(я не уверен действительно ли это проблема, но выглядит нехорошо); 2) из-за тета-функций (которые ограничивают решения внутри "своей" ямы) появляются дельта-функции, да ещё и с совпадающими аргументами - надо это всё регуляризировать, но как именно - не вполне понятно (возможны варианты - подвигать туда-сюда концы обрезаний, или сделать обрезания плавными, или ещё как (и при любом варианте "сбивается" ортонормировка)); 3) есть предчувствие, что если ничего не предпринять (не модифицировать базис), то "перекрытие" функций (точнее "межямные" матричные элементы) будут неправильными (малыми).
Что делать и как всё это преодолевать я пока не могу придумать. То ли как-то модифицировать базис, то ли надо как-то по-другому разбивать задачу на "первоначально несвязанные" области (например, модифицировать граничные условия), то ли переходить к фурье-образам и мудрить с ними.