Уважаемый
sup!
Я решил для случая

в
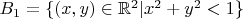
Решение в данной случае имеет вид:

Так как у нас

, то решение принимает вид:

поскольку

Сравнив коэффициенты Фурье левой и правой части получаем, что:

и

, а остальные обнуляются
Подставляя все обратно получаем, что:

Надеюсь, что нигде не накосячил.
А как для случая

решить я что-то не знаю.
Помогите пожалуйста.