Подмножества и подпространства

[zychnyy]

*Проверить, является ли подмножество ${L}_{1}$ линейного пространства $L$ подпространством.
$1)\ L=V_3,\ L_1=\{ a\in V_3:a\parallel \pi \} $, где $\pi $- заданная плоскость.

(Оффтоп)

Тут все понятно - $L_1\triangleleft L$.

$2)\ L=V_3,\ L_1=\{ a\in V_3:|a|=1\} $.

(Оффтоп)

Пусть $b=\alpha a$. Тогда $|b|=|\alpha ||a|\neq 1$, при $\alpha =0\ \Rightarrow \ L_1\bar{\triangleleft } L$.

$3)\ L=R^n,\ L_1=\{ a=(a_1,...,a_n)\in R^n:a_1+...+a_n=0\} $.

(Оффтоп)

Ведь $L_1\triangleleft L\ ?$

$4)\ L=R^\infty $ - линейное пространство последовательностей,
$L_1=\{ \{ a_n\} \in R^\infty :\{ a_n\} \} $ сходится $\} $.

(Оффтоп)

Ну здесь прозрачно - $L_1\triangleleft L$.

$5)\ L=R^\infty $, $L_1=\{ \{ a_n\} \in R^\infty :\lim\limits_{n\to \infty } a_n=0\} $.

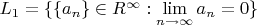
(Оффтоп)

Требования подпространства выполняются - $L_1\triangleleft L$.

$6)\ L=R^\infty $, $L_1=\{ \{ a_n\} \in R^\infty :\{ a_n\} $ монотонно не убывает$\} $.

(Оффтоп)

Пусть $b_n=-a_n$. Тогда $b_n>{b}_{n+1}$ и $L_1\bar{\triangleleft }L$.

Буду благодарен за проверку и замечания.

[arseniiv]

3 — да, почему сомнения? При сложении складывается ноль с нулём, при масштабировании ноль умножается на число.

[zychnyy]

(Оффтоп)

Цитата:

3 — да, почему сомнения?

arseniiv тривиальность напугала.