Добрый день!
В одном иностранном математическом сообществе нашёл такой вопрос и такой ответ:
Вопрос:
Цитата:
Find positive and negative indecies of inertia of a quadratic form
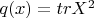
on the
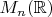
(vector space of square matrices).
Перевод:
Цитата:
Найдите положительные и отрицательные индексы инерции квадратичной формы
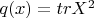
на
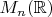
(векторное пространство квадратных матриц).
Ответ:
Let
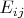
be the matrix whose

-th entry is

and all other entries zero. . Since
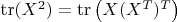
, the matrix of the quadratic form

with respect to the standard basis
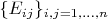
of
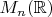
is the [commutation matrix][1]
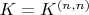
. (That is,

is the
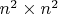
real symmetric permutation matrix such that
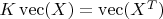
.) Clearly, for each

,
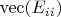
is an eigenvector of

corresponding to the eigenvalue

(because
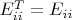
). Also, for all
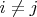
,
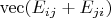
is an eigenvector of

corresponding to the eigenvalue

and
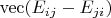
is an eigenvector of

corresponding to the eigenvalue

. Since these vectors form a basis of
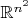
, we conclude that

has
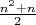
positive eigenvalues and
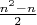
negative eigenvalues.
[1]:
http://en.wikipedia.org/wiki/Commutation_matrixС вопросом всё вполне ясно. Но вот не уверен, что правильно понимаю ответ.
Привожу мой перевод и прошу исправить меня, или перефразировать те моменты, которые переведены "не очень хорошо".
===================
Пусть
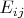
- матрица, элемент

которой равен единице, а всё остальные - нулю. Так как
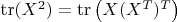
, матрица квадратичной формы

в стандартном базисе
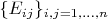
пространства
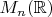
является [commutation matrix][1]
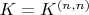
. (это такая симметричная действительная матрица перестановок

размером
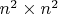
, что
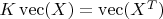
.) Очевидно, для каждого

,
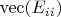
является собственным вектором

соответствующим собственному значению

(так как
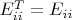
). Так же, для всех
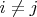
,
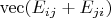
является собственным вектором

соответствующим собственному значению

и
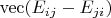
является собственным вектором

соответствующим собственному значению

. Так как эти векторы являются базисом в
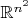
, можно сделать вывод, что у

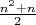
положительных собственных значения
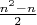
отрицательных.
[1]:
http://en.wikipedia.org/wiki/Commutation_matrix