Давайте рассмотрим бублик, т.е. тор. Пусть этот тор будет резиновым (у резины модуль упругости меньше). Геометрическое место центров масс поперечных сечений тора образует окружность радиуса

. Назовём этот радиус радиусом тора. Радиус поперечного сечения тора обозначим

.
Если мы будем увеличивать внешнее давление, то тор начнёт сжиматься. Будут уменьшаться его радиусы

и

. Если внешнее давление уменьшать, то эти радиусы начнут увеличиваться.
Проведём через ось симметрии тора две плоскости с небольшим углом
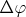
между ними и рассмотрим два близких поперечных сечений тора этими плоскостями. Если увеличивать внешнее давление, то длина окружности радиуса

начнёт уменьшаться, так как уменьшается сам радиус

. Расстояние между соответствующими поперечными сечениями тоже начнёт уменьшаться.
Еcли часть резины между этими сечениями вырезать и удалить, то начнёт уменьшаться зазор между торцами (сечениями тора). Вот теперь, если один конец тора вблизи сечения приклеить к столу, то второе сечение, свободное, начнет перемещаться и поворачиваться. Следовательно, если к свободному концу тора приклеить стрелку, то она тоже начнёт поворачиваться.
У Вас есть возражения по поводу этих рассуждений?