Ну давайте возьмём функции наугад. Пусть

,
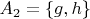
. Тогда для (а)
![$K_1 = [\{g\}] = \{\mathrm{id}, g, gg, ggg, \ldots\}$ $K_1 = [\{g\}] = \{\mathrm{id}, g, gg, ggg, \ldots\}$](https://dxdy-02.korotkov.co.uk/f/1/e/3/1e3b0bacc75770f50105115735e2d00e82.png)
,
![$K_2 = [\{f, g\}] \cap [\{g, h\}] = \{\mathrm{id}, f, g, fg, gf, \ldots\} \cap \{\mathrm{id}, g, h, gh, hg, \ldots\} = \,?$ $K_2 = [\{f, g\}] \cap [\{g, h\}] = \{\mathrm{id}, f, g, fg, gf, \ldots\} \cap \{\mathrm{id}, g, h, gh, hg, \ldots\} = \,?$](https://dxdy-01.korotkov.co.uk/f/4/c/5/4c5d9615040c6a5a877c5555abb9b8be82.png)
(Заметьте, никаких особых свойств булевых функций тут вообще не использовано. Может, в задании (б) они уже понадобятся.)

— тождественная функция. Если в вашем определении замыкания она в него не входит, вычёркиваем и забываем.
-- Пт мар 08, 2013 21:07:41 --Это ещё не доказательство, но превратится в него, если рассмотреть каждое из

,

,

.