Здравствуйте, не могли бы вы подсказать какую-то литературу на русском языке (или на английском - если очень хорошо объяснено, достаточно дискретного случая) по т.н. coupling method ' у. Еще один вариант перевода - "метод склеивания". Или может есть какой-то правильный перевод, но я о о нем не знаю. Мне дали классическую в этом плане книжку torgny lindvall - lectures on coupling method 1992 года:
http://sci-prew.inf.ua/other/Torgny%20Lindvall%20-%20Lectures%20on%20the%20Coupling%20Method.pdf В принципе, чтобы понять что это, можно прочитать пару страниц вступления.
Для двух вероятностных мер

и

на измеримом пространстве

(соответственно пр-во элем событий и сигма-алгебра), мы назовем их каплингом вер. меру
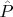
на

, такую, что

и

, где

для

. Тогда

и

- маргинальные распределения
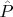
. (1)
Для случайных величин

мы будем называть каплингом конструкцию

, в которой

- каплинг

и

в смысле (1).
Пусть у нас есть некоторая случайная последовательность

. Мы берем вторую какую-то последовательность

, такую, что существует конечное время

(для дискретного случая), такое, что

.
Доказывается, что выполняется неравенство каплинга:

Или с операторами сдвига:

Понятно, нас интересует сходимость.
В начале книги рассмотрены три простых примера применения.
Может кто-нибудь знает какую-то новую литературу, может учебники, где есть этот метод?