Численное решение нелинейной краевой задачи

[Ketsyki]

Здравствуйте. Запутался в решении нелинейной краевой задачи.

Пусть есть
$y(x)''=f(x,y,y')$
$0<x<1$
$y(0)=A, y(1)=B$

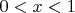
Сперва я свел исходное уравнение к системе нелинейных алгебраических уравнений используя аппроксимацию
$\frac{d^2y}{dx^2} = \frac{y(x_{i+1}) - 2y(x_i) + y(x_{i-1})}{h^2}$
$x_i = x_0+ih$

Получил систему вида:
$y_{i+1}-2y_i+y_{i-1}=h^2f_i$
$i=1,2,...,n-1$
$y_0=A$
$y_n=B$
$h=\frac{A-B}{n}$

Потом решил эту систему методом Ньютона и получил значения $y_1, y_2,...,y_{n-1}$

И тут у меня 2 вопроса:
1. Что дальше делать?
2. Как можно выбирать начальное приближение? Т.к. я писал программу, то приближение мог выбирать любое, просто число итераций надо увеличивать.